Характеристики детерминированных сигналов. Представление произвольного сигнала в виде суммы элементарных колебаний, страница 13

Влияние неидеальности фильтра нижних частот, применяемого для восстановления сигнала по его отсчётам, проявляется в том, что на его выходе выделяется не только центральная часть спектра  (см. рис. 28), но и частично сигналы соседних спектров, даже когда они не перекрываются. Очевидно, что в этом случае повышение частоты отсчётов позволяет лучше разнести спектры и уменьшить нежелательное проникновение составляющих частот соседних спектров. Очевидно также, что чем ближе к идеальным характеристикам фильтра нижних частот в схеме рис. 27, тем меньше влияние рассмотренных выше практических ограничений.

Физическая реализуемость фильтров. Осуществимость того или иного фильтра можно определить по его передаточной функции . Необходимым, но недостаточным условием физической реализуемости фильтра, согласно критерию Пэли-Винера, является конечность интеграла

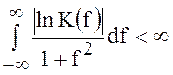.                                                                                 (123)

Например, фильтр с прямоугольной передаточной функцией нереализуем, так как  за пределами полосы пропускания равен бесконечности. Нереализуем также и фильтр колоколообразной передаточной функцией, так как, хотя отношение числителя и знаменателя стремится к конечному пределу, интеграл равен бесконечности.

Однако сказанное не означает, что нельзя реализовать фильтр с передаточной функцией, близкой к идеальной прямоугольной форме. Например, передаточную функцию, близкую к идеальной прямоугольной форме, можно получить с помощью фильтра, состоящего из большого числа колебательных контуров.

1.12. Представление сигналов на плоскости комплексной переменной

Анализ прохождения сигналов в линейных цепях, описываемых комплексным коэффициентом передачи, существенно облегчается при использовании методов контурного интегрирования на плоскости комплексной переменной . Переход от действительной переменной  к комплексной переменной  позволяет полностью устранить ограничения, вытекающие из требования абсолютной интегрируемости функций  при её представлении в частотной области.

Пусть функция , задана на временном промежутке .

В преобразованиях Фурье () и () совершим переход от действительной переменной  к комплексной переменной . Для этого помножим  на множитель , где положительную константу  выбираем таким образом, чтобы функция  удовлетворяла условию абсолютной интегрируемости.

Произведению  соответствует спектральная плотность

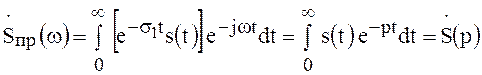.                                  (124)

Правая часть последнего выражения , являющаяся функцией комплексной переменной  называется односторонним преобразованием Лапласа.

Представим функцию  в форме обратного преобразования Фурье:

.

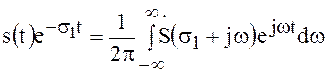Переходя под интегралом к переменной , получим

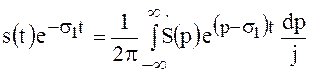, откуда 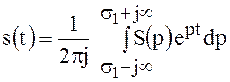.                                                                 (125)

Выражение (125) позволяет при заданном изображении  однозначно восстановить оригинал  для , по аналогии с выражением (), и называется обратным преобразованием Лапласа.

Сравнение выражений (ОПФ) и (ОПЛ) показывает, что переход от вещественной переменной  к комплексной переменной равносилен изменению пути интегрирования. В выражении (ОПФ) интегрирование проводится по действительной оси  (рис. 29a)., а в выражении (ОПЛ) – по прямой, проходящей параллельно мнимой оси  на расстоянии  справа от неё (рис. 29б).

a/                                                                      б/

Рис. 29

Значение константы  определяется характером подынтегральной функции в выражении (125): путь интегрирования должен проходить правее полюсов этой функции.

Добавлением к прямой  дуги бесконечно большого радиуса можно образовать замкнутый контур интегрирования (рис. 29 б). Чтобы добавление этой дуги не изменяло значение интеграла, необходимо руководствоваться следующим правилом: контур должен быть расположен при  в левой полуплоскости комплексной переменной р, а при t < 0 – в правой полуплоскости.