Характеристики детерминированных сигналов. Представление произвольного сигнала в виде суммы элементарных колебаний, страница 26

При составлении определителей по указанной схеме коэффициенты с индексом, превышающим степень характеристического уравнения, заменяются нулями. Поэтому для уравнения четвёртой степени получаются следующие определители:

, , , .

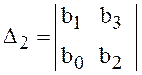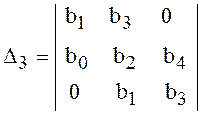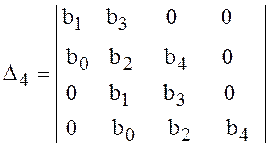Видно, что все последовательные определители являются главными диагональными минорами определителя . Так как последний столбец содержит только один отличный от нуля элемент , расположенный на главной диагонали, то выполняются равенства:

.

Отсюда следует, для характеристического уравнения  степени выполняются следующие равенства:

, ,              , .

Так, для характеристического уравнения  степени

, , для уравнения  степени

, .

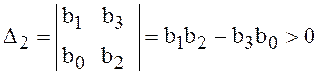Достоинство критерия Рауса-Гурвица – относительная простота вычислений. Недостатком является то, что область применения этого критерия ограничена линейными цепями с сосредоточенными параметрами, поскольку только в этом случае передаточная функция представляет частное двух многочленов.

Геометрический критерий устойчивости (Критерий Найквиста)

В характеристическом уравнении () произведение                                                                                                    ()

есть не что иное, как передаточная функция последовательного соединения двух звеньев – усилителя и четырёхполюсника обратной связи. Обычно передаточную функцию  называют передаточной функцией системы с разомкнутой обратной связью.

Выражение () описывает отображение комплексной плоскости р на другую комплексную плоскость . Если , , - корни характеристического уравнения , , - корни характеристического уравнения , то на комплексной плоскости  всем этим точкам будет соответствовать единственная точка . Отсюда вытекаеткритерий устойчивости, позволяющий судить о возможности самовозбуждения системы с обратной связью: если образ правой полуплоскости комплексной переменной р при отображении вида () содержит точку , то система с замкнутой обратнойсвязью неустойчива.

Роль параметра функции  играет частота , которая изменяется от  до . Кривая зависимости  называется амплитудно-фазовой  характеристикой (АФХ) разомкнутой системы. В практических случаях модули коэффициентов передачи  стремятся к нулю с ростом частоты. Поэтому АФХ проходит через точку . Кроме того, АФХ симметрична относительно вещественной оси на плоскости , поскольку . Очевидно, что АФХ для физически реализуемых систем представляют замкнутые кривые в плоскости .

В теории функций комплексного переменного [] показывается, что при отображении вида () образом правой полуплоскости  является внутренняя область, охватываемая кривой АФХ. Критерий устойчивости, вытекающий из описанного построения, известен под названием критерия Найквиста: если АФХ разомкнутой системы охватывает точку (1, j0), то замкнутая система устойчива.

Если исходный контур на плоскости р задан в виде контура на рис.  a соответствующий ему контур на плоскости Н (рис.  б) называется годографом функции .

a/                                                                     b/

Рис.

Обходу контура С на рис.  a/ в положительном направлении (против часовой стрелки) соответствует обход годографа  при изменении частоты от  до , т.е. также против часовой стрелки (рис. б).

Очевидно, что вся правая плоскость р преобразуется на плоскости Н во внутреннюю область годографа. Следовательно, если годограф передаточной функции разомкнутого тракта не охватывает точку 1, j0, то при замыкании цепи обратной связи система устойчива, в противном случае система неустойчива.

3.8. Прохождение АМ колебания через резонансный усилитель

На вход одноконтурного резонансного усилителя, изображённого на рис.  , поступает АМ колебание

.                                                ()

Требуется определить колебание на выходе усилителя.

Колебательный контур усилителя, является инерционной цепью, что и приводит к изменению параметров выходного колебания.