График такой импульсной функции приведен на рис. 22.
Параметр ![]() , равный по модулю коэффициенту наклона ФЧХ
фильтра
, равный по модулю коэффициенту наклона ФЧХ
фильтра  , определяет задержку
во времени максимума функции
, определяет задержку
во времени максимума функции ![]() . Ясно,
что данная модель фильтра тем точнее отображает свойства физически реализуемой
системы, чем больше величина задержки во времени
. Ясно,
что данная модель фильтра тем точнее отображает свойства физически реализуемой
системы, чем больше величина задержки во времени ![]() .
.
Рис. 22
Рассмотрим случай, когда на вход рассматриваемого фильтра
поступает напряжение импульса прямоугольной формы с амплитудой ![]() , действующего в пределах
времени от
, действующего в пределах
времени от ![]() до
до ![]() (рис. 23).
(рис. 23).
Рис. 23
Спектр одиночного прямоугольного импульса на основании теоремы сдвига времени равен
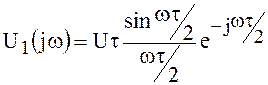 .
.
Спектр сигнала на выходе фильтра
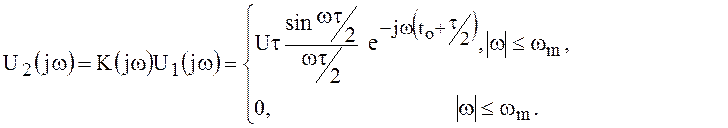
В соответствии с формулой обратного преобразования Фурье имеем
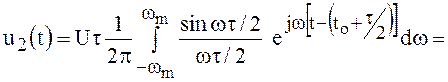
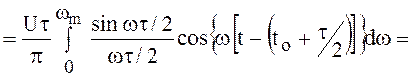
 (110)
(110)
Введя обозначения ![]() и
и ![]() , получим
, получим
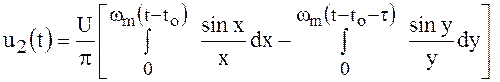 .
.
Следовательно,
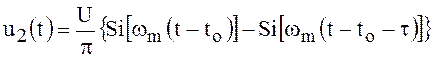 ,
(111)
,
(111)
где 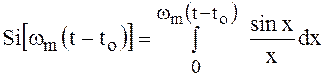 и
и  .
.
1.11. Сигналы на выходе идеального полосового фильтра
Связь между полосой пропускания идеального полосового фильтра и временем установлением сигнала. Рассмотрим случай, когда на вход идеального полосового фильтра с передаточной функцией, показанной на рис. 24 a, поступает высокочастотное колебание, огибающая которого имеет вид прямоугольного импульса (рис. 24 b).
a/ b/
Рис. 24
Пусть несущая частота ![]() высокочастотного
колебания совпадает со средней частотой полосового фильтра
высокочастотного
колебания совпадает со средней частотой полосового фильтра ![]() .
.
Можно показать, что огибающая высокочастотного
колебания на выходе полосового фильтра совпадает с напряжением на выходе
фильтра нижних частот, имеющего граничную частоту 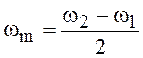 . Поэтому амплитуда
высокочастотного напряжения на выходе полосового фильтра
. Поэтому амплитуда
высокочастотного напряжения на выходе полосового фильтра
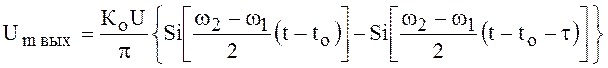 .
(112)
.
(112)
Огибающую прямоугольного радиоимпульса можно рассматривать как сумму двух огибающих (рис. 25).
Рис. 25
Полагая в (112) ![]() , получим
, получим
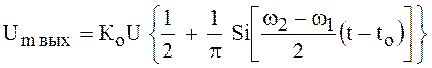 ,
,
Обозначая ![]() ,
имеем
,
имеем
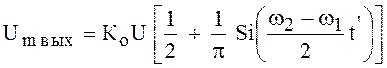 .
(113)
.
(113)
Изменение огибающей высокочастотного на выходе идеального полосового фильтра при включении высокочастотного напряжения на его входе показано на рис. 26.
Рис. 26
Найдём время установления амплитуды от уровня 0,1 до
уровня 0,9 установившегося значения ![]() .
Как видно из рис. 26,
.
Как видно из рис. 26,
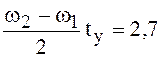 , откуда следует, что время установления
, откуда следует, что время установления
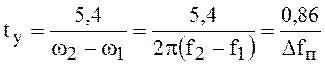 ,
(114)
,
(114)
где ![]() -
полоса пропускания полосового фильтра.
-
полоса пропускания полосового фильтра.
Связь между полосой пропускания идеального полосового фильтра и максимальной амплитудой выходного импульса. Выражение (112) для амплитуды радиоимпульса на выходе идеального полосового фильтра можно представить в следующем виде
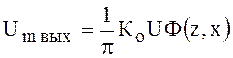 ,
(115)
,
(115)
где ![]() ;
; 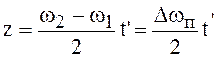 ;
; 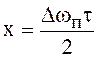 .
.
Для определения максимального значения амплитуды
выходного напряжения ![]() необходимо
найти значение z, при котором
необходимо
найти значение z, при котором 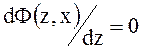 .
.
Дифференцируя ![]() по z решая
относительно z уравнение, получим
по z решая
относительно z уравнение, получим
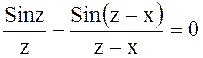 , находим
, находим  .
.
Подставляя это значение в (115), получим
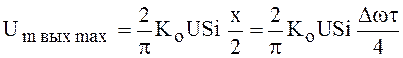 .
(116)
.
(116)
При малых значениях ![]() можно полагать, что
можно полагать, что ![]() . Тогда
. Тогда
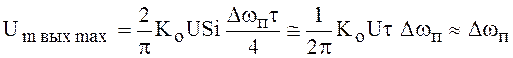 .
(117)
.
(117)
Следовательно, при очень узкой полосе пропускания идеального полосового фильтра амплитуда радиоимпульса на его выходе пропорциональна его полосе пропускания.
1.11. Теорема Котельникова
В теории и практике сигналов широко используется
теорема Котельникова (теорема отсчётов): если наивысшая частота в спектре
функции сигнала ![]() меньше,
чем
меньше,
чем ![]() , т.е.
, т.е. ![]() на частотах
на частотах ![]() >
> , то функция
, то функция ![]() полностью
определяется последовательностью своих значений в моменты, отстоящие друг от
друга не более чем на шаг
полностью
определяется последовательностью своих значений в моменты, отстоящие друг от
друга не более чем на шаг  секунд.
секунд.
В соответствии с этой теоремой сигнал ![]() , ограниченный по спектру
максимальной частотой
, ограниченный по спектру
максимальной частотой ![]() , можно
представить рядом:
, можно
представить рядом:
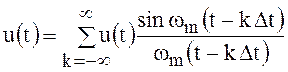 ,
(118)
,
(118)
где ![]() - максимальная
частота спектра передаваемой функции.
- максимальная
частота спектра передаваемой функции.
Доказательство теоремы. Пусть непрерывная функция времени ![]() имеет спектр,
ограниченный частотой
имеет спектр,
ограниченный частотой ![]() .
.
Используя обратное преобразование Фурье, запишем эту функцию в виде
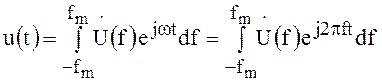 .
(119)
.
(119)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.