Характеристики детерминированных сигналов. Представление произвольного сигнала в виде суммы элементарных колебаний, страница 7

Интеграл под знаком предела представляет собой энергию отрезка сигнала  длительностью Т, т.е. 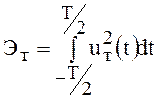, поэтому для мощности непериодического сигнала получим

.

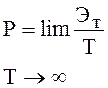Используя (72), можно записать

,

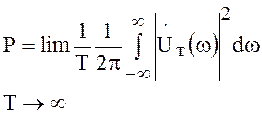где  - спектр отрезка сигнала длительностью Т.

Поменяв местами операции интегрирования и предела, имеем

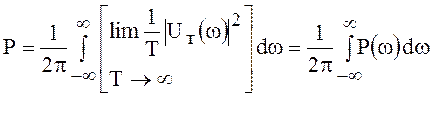,                                      (71)

где .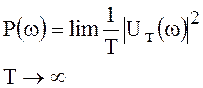

В такой форме представление о спектре мощности можно использовать не только для детерминированных сигналов, но и для случайных сигналов. Спектр мощности  сигнала  равен мощности его составляющих в полосе 1 Гц в окрестности частоты .

1.6. Примеры определения спектров непериодических колебаний

Нельзя непосредственно применять преобразование Фурье к скачку напряжения или к другой функции, не убывающей на бесконечности. Однако можно ограничить продолжительность функции любым достаточно большим отрезком времени или умножить такую функцию на медленно затухающую экспоненту, удовлетворив тем самым условию абсолютной интегрируемости.

Дельта-функция (единичный импульс). Дельта-функция переменной времени (рис. 13) определяется следующими равенствами:

;

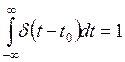.                                                                                      (73)

При  дельта-функция имеет бесконечное значение.

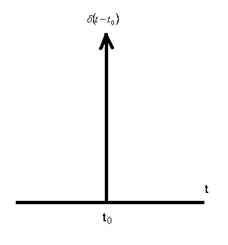
Рис. 13

Единичный импульс можно рассматривать как предел, к которому стремится импульс, имеющий форму прямоугольника, треугольника, колокола и т.д., при стремлении длительности  к нулю.

Согласно (73)

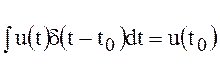.                                                                           (74)

Единичный импульс напряжения (рис. 14)

;

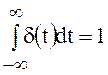.                                                                                      (73)

имеет спектр

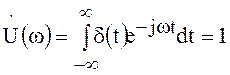.                                                                         (75)

а                                                              б  

Рис. 14

Итак, спектр дельта–функции  вещественен и равен единице для всех частот. Из этого следует, что ФЧХ этого спектра равна нулю для всех частот.

Обратное преобразование Фурье для дельта-функции приводит к интегралу

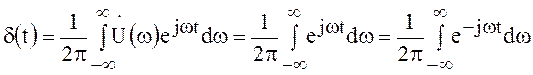.                     (75)

Рассмотрим свойства дельта функции в частотной области . Всё, что ранее было сказано относительно , можно отнести и к  при замене t на  и  на t, т.е. используется свойство взаимной обратимости частоты и времени в преобразованиях Фурье.

Определение  по аналогии с  имеет вид

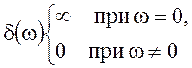 при одновременном выполнении условия

.                                                                                           (76)

По аналогии с (75) можно написать

.                                                       (78)

Скачок напряжения. Скачком напряжения, или единичной функцией (рис. 14), называется функция, определяемая выражением

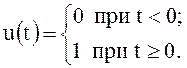                                                                                 (79)

Рис. 14

Эту разрывную функцию можно представить в виде суммы

,

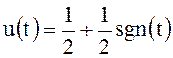где

Найдём спектр такой функции. Непосредственно с помощью формулы прямого преобразования Фурье сделать этого нельзя, так как такая функция не удовлетворяет условию абсолютной интегрируемости. Нескольку видоизменим единичную функцию, умножив её на затухающую экспоненту

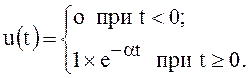                                                                      (80)

Спектр такой функции

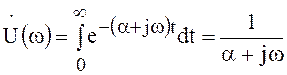.                                                               (81)

Спектр единичной функции найдём путём перехода к пределу

.

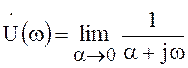Непосредственный переход к пределу, согласно которому , справедлив при всех частотах, кроме значения , когда требуется более тщательное рассмотрение.

С этой целью выделим в спектре экспоненциального сигнала действительную и мнимую части:

.|

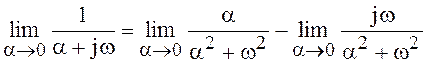При  первое слагаемое в правой части этого выражения равно нулю на всех частотах, кроме , где оно обращается в бесконечность, а площадь под функцией 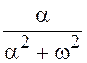 равна постоянной величине

.

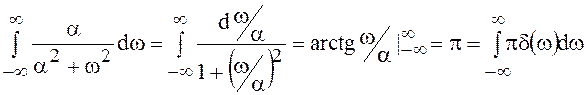Поэтому предел первого слагаемого равен 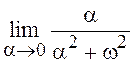=. Пределом второго слагаемого является . Окончательно получим