Характеристики детерминированных сигналов. Представление произвольного сигнала в виде суммы элементарных колебаний, страница 3

.                                                                            (28)

Модуль  является чётной функцией дискретной переменной n (частоты), а аргумент  - нечётной: , .

Выражение (20) можно представить в следующем виде:

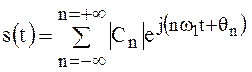                                                                     (29)

От комплексной формы ряда Фурье нетрудно перейти к тригонометрической форме. Выделим в ряде (29) пару слагаемых, соответствующих какому–либо фиксированному значению n:

.

Векторная диаграмма этих комплексных составляющих ряда представлена на рис. 1.1

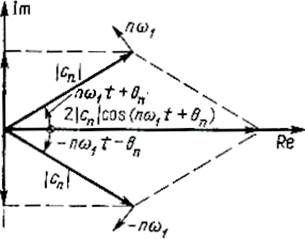
Рис. 1.1

Векторы длиной  вращаются с угловой частотой  во взаимно противоположных направлениях. Сумма проекций этих векторов на действительную ось даёт вещественную функцию , а сумма проекций этих же векторов на мнимую ось равна нулю.

Поэтому, при переходе к тригонометрической форме ряд (29) следует записать следующим образом:

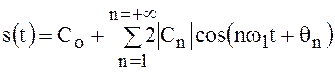.                                                       (30)

Ряд Фурье (30) можно представить и в следующем виде:

.   (32)

Здесь .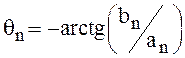

Из сравнения выражений (30) и (32) видно, что амплитуда n-й гармоники  связана с коэффициентом  ряда (30) выражениями

, а , .                                                    (33)

Для коэффициентов ряда  и , используя формулы (32) и (33) можно записать:

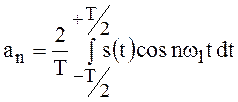,                                                                       (34)

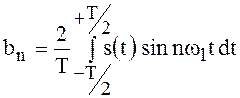.                                                                       (35)

Если сигнал  - чётная функция времени, т.е. , то в ряде (32) остаются только косинусоидальные члены, так как коэффициенты  в соответствии с  обращаются в нуль. Для нечётной функции , наоборот, в нуль обращаются коэффициенты , и ряд состоит только из синусоидальных членов.

Амплитудная и фазовая характеристики, т.е. модули и аргументы комплексных коэффициентов ряда Фурье, полностью определяют структуру частотного спектра периодического сигнала.

Постоянная составляющая периодического сигнала – напряжения

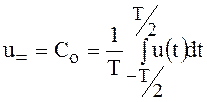.                                                                             (36)

Амплитуда n-ой гармоники напряжения

.                                                                                  (37)

Действующее значение n-ой гармоники напряжения

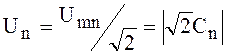.                                                                          (38)

При рассмотрении энергетических характеристик периодического сигнала основной интерес представляют средняя мощность и распределение этой мощности между отдельными гармониками. Средняя мощность сигнала, заданного на всей временной оси, вследствие его периодичности, совпадает с мощностью, средней за период. Поэтому можно воспользоваться формулой (22), в которой под коэффициентами  следует подразумевать коэффициенты ряда (30), а под интервалом ортогональности  и квадратом нормы  - величину T [см. (13)].

Используя формулу 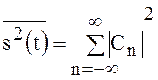 и учитывая, что

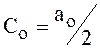 и 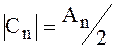, найдём мощность, выделяемую на сопротивлении нагрузки в 1 Ом

.

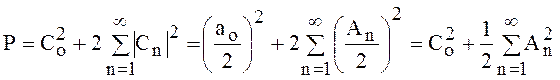Если  представляет собой ток , то при прохождении его через сопротивление r выделяется средняя мощность

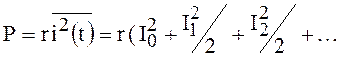),                                                     (39)

где 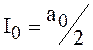 - постоянная составляющая, а  амплитуда n-й гармоники тока .

Итак, полная средняя мощность периодического сигнала равна сумме средних мощностей, выделяемых отдельно постоянной составляющей и гармониками.

1.3. Примеры определения спектров периодических колебаний

Прямоугольные периодические импульсы (меандр).Так как  (рис. 1.2) является чётной функцией, то ряд содержит только косинусоидальные члены с коэффициентами :

.                                  (40)

Рис. 1.2

Спектр амплитуд  чётной функции  показан на рис. 1.3.

Рис. 1.3

С увеличением числа суммируемых гармоник сумма ряда приближается к функции  всюду кроме точек вблизи разрыва функции, где образуется выброс. При  величина этого выброса равна , т.е. сумма ряда отличается от заданной на 18%. Несмотря на то, что в рассматриваемом случае ряд Фурье не сходится к разлагаемой функции  в точках её разрыва, ряд сходится в среднем, поскольку при  выбросы являются бесконечно узкими и не вносят никакого вклада в сумму (10).