Характеристики детерминированных сигналов. Представление произвольного сигнала в виде суммы элементарных колебаний, страница 19

Таким образом, при угловой модуляции спектр радиосигнала состоит из бесконечного числа частот , расположенных попарно симметрично относительно несущей частоты  и отличающихся от последней на частоту , где k – любое целое число. Амплитуда k-ой боковой составляющей , где  - амплитуда немодулированного колебания. Отсюда следует, что вклад различных боковых частотных составляющих в суммарную мощность колебания определяется величиной индекса модуляции m.

Если m « 1, то можно пренебречь высшими гармоническими составляющими так, как  «. Поэтому можно воспользоваться следующим приближением:

.

Учитывая, что при малых значениях m  и

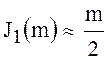, можно записать

.

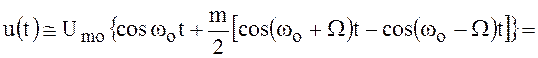
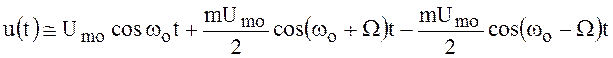Как следовало ожидать полученное выражение совпадает с выражением однотонального радиосигнала с угловой модуляцией ().

С ростом индекса модуляции расширяется полоса частот, занимаемая ЧМ (ФМ) радиосигналом (рис. 13.).

Рис. 13

Обычно полагают, что допустимо пренебречь всеми спектральными составляющими с номерами k > m+1. Отсюда следует оценка практической ширины ЧМ (ФМ) радиосигнала по формуле:

.                                                                          ()

Как правило, практически используемые радиосигналы с угловой модуляцией характеризуются условием . В этом случае .

Поскольку , то практическая ширина спектра оценивается формулой .                                                                                       ()

Так как ширина спектра угловой модуляции при k > m+1 существенно возрастает, то угловую модуляцию называют широкополосной. Однако при этом 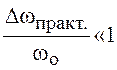 за счёт выбора  в диапазоне более высоких частот (УКВ диапазон).

Угловая модуляция при негармоническом модулирующем сигнале. Когда модулирующий сигнал не является гармоническим, то проявляются интересные особенности радиосигнала с угловой модуляцией, отличные от свойств АМ радиосигнала.

Рассмотрим для этого простейший случай угловой модуляции двумя НЧ сигналами:

.                                            ()

Предположим, что парциальные индексы модуляции  и  малы настолько, что справедливы следующие приближённые выражения для гармонических функци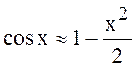й:

 и .

Выполнив несложные и громоздкие преобразования, можно представить рассматриваемый радиосигнал с угловой модуляцией в следующем виде:

.                                              ()

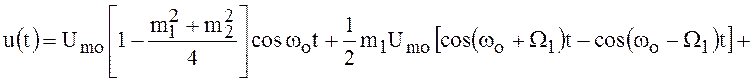
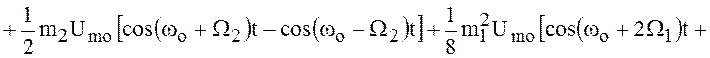
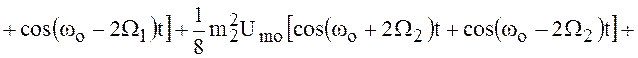
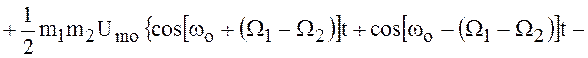
В спектре рассматриваемого радиосигнала с угловой модуляцией, кроме составляющих боковых частот , , , , , присутствуют так называемые комбинационные частоты  с четырьмя возможными знаками. Амплитуды этих составляющих зависят от произведения индексов модуляции , что характеризуют взаимодействие отдельных составляющих модулирующих сигналов.

Следовательно, при прочих равных условиях спектр радиосигнала с угловой модуляцией значительно богаче спектра аналогичного АМ радиосигнала. Радиосигнал с угловой модуляцией называют модуляцией нелинейного типа так как имеется взаимодействие отдельных составляющих модулирующих сигналов.

Глава 2

ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ СИГНАЛОВ

В этом разделе рассматриваются шумы, проявляющиеся в виде электрических колебаний, представляющих собой случайный сигнал. Рассматриваются статистические характеристики шумов.

2.1. Общие определения

Информация, передаваемая по каналу связи или полученная в результате измерения, заключена в сигнале. До приёма сообщения (до измерения) сигнал следует рассматривать как случайный процесс, характеризуемый совокупностью (ансамблем) функций времени. Одна из этих функций времени, ставшая полностью известной после приёма (измерения) сообщения называется реализацией случайного процесса. Эта реализация является уже не случайной, а детерминированной функцией времени.

Важной характеристикой случайного процесса является одномерный закон распределения вероятностей.

Совокупность функций , , , , , образующих случайный процесс , изображена на рис. 2.1. Значения, которые могут принимать отдельные функции в момент времени , образуют совокупность случайных величин  , , , , .