
Рис. 2.2
Вероятность того, что величина случайная величина ![]() при приёме (испытании) попадает в какой-либо интервал
(a,b) (рис. 2.2), определяется выражением
при приёме (испытании) попадает в какой-либо интервал
(a,b) (рис. 2.2), определяется выражением
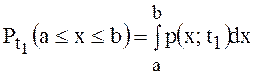 .
(4.1)
.
(4.1)
Функция ![]() называется
интегральной вероятностью, а функция
называется
интегральной вероятностью, а функция ![]() , представляющая собой дифференциальный закон распределения
случайной величины
, представляющая собой дифференциальный закон распределения
случайной величины ![]() , - одномерная плотность вероятности.
, - одномерная плотность вероятности.
Функция ![]() является статистической характеристикой случайного сигнала
является статистической характеристикой случайного сигнала ![]() непрерывного типа,
могущего принимать любое значение в некотором интервале. Для любой функции
непрерывного типа,
могущего принимать любое значение в некотором интервале. Для любой функции ![]() должно выполняться
равенство
должно выполняться
равенство
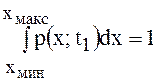 ,
(4.2)
,
(4.2)
где ![]() и
и ![]() - минимальное и
максимальное значения
- минимальное и
максимальное значения ![]() .
.
Если ![]() является
случайной величиной дискретного типа и может принимать любое из конечного числа
дискретных значений, то (4.2) следует заменить суммой
является
случайной величиной дискретного типа и может принимать любое из конечного числа
дискретных значений, то (4.2) следует заменить суммой
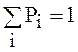 ,
(
,
(![]()
где ![]() - вероятность,
соответствующая дискретному значению случайной величины
- вероятность,
соответствующая дискретному значению случайной величины ![]() .
.
Задание одномерной плотности вероятности ![]() позволяет произвести
статистическое усреднение, как самой величины
позволяет произвести
статистическое усреднение, как самой величины ![]() , так и любой функции
, так и любой функции
![]() . Под статистическим
усреднением подразумевается усреднение
. Под статистическим
усреднением подразумевается усреднение ![]() ансамблю в
фиксированный момент времени.
ансамблю в
фиксированный момент времени.
Глава 3
АКТИВНЫЕ ЛИНЕЙНЫЕ ЦЕПИ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ
В данном разделе приводятся общие сведения об активных линейных цепях (АЛЦ). Активный характер радиотехнической цепи обусловлен применением в них усилительных элементов: транзисторов, электронных ламп, интегральных микросхем и.т. Для активных линейных цепей справедлив принцип наложения.
3.1. Активная линейная цепь. Частотные и временные характеристики
Рассмотрим АЛЦ, представляя её в виде четырёхполюсника (рис. 3.1.).
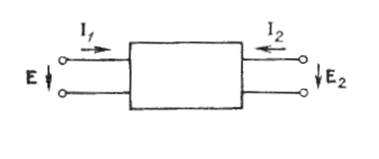
Рис. 3.1
Основная часть энергии сигнала распространяется с входа на выход четырёхполюсника, обратное прохождение сигнала существенно меньше прямого. Поэтому принцип взаимности для АЛЦ неприменим.
Линейная цепь активна, если при гармоническом входном сигнале средняя мощность сигнала на выходе больше средней мощности на входе, т.е. коэффициент усиления по мощности больше единицы.
Исчерпывающей характеристикой АЛЦ в частотной области
является её передаточная функция ![]() :
:
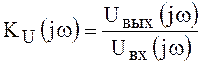 -
передаточная функция по напряжению;
-
передаточная функция по напряжению;
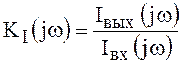 -
передаточная функция по току;
-
передаточная функция по току;
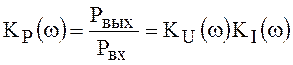 -
передаточная функция по мощности.
-
передаточная функция по мощности.
Передаточную функцию удобно представить в показательной форме
![]() ,
(3.1)
,
(3.1)
где  и
и 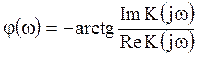 - модуль и фаза передаточной
функции
- модуль и фаза передаточной
функции ![]() .
.
Другой исчерпывающей характеристикой АЛЦ является её
импульсная характеристика ![]() ,
используемая для описания АЛЦ во временной области.
,
используемая для описания АЛЦ во временной области.
Под импульсной характеристикой АЛЦ подразумевается её отклик (реакция) на воздействие, имеющее вид единичного импульса (дельта-функции).
Выражение выходного напряжения АЛЦ можно получить по
формуле ОПФ, полагая в ней ![]() ,
,
![]() и
и ![]()
 .
(3.2.)
.
(3.2.)
Передаточная функция является прямым преобразованием Фурье импульсной характеристики
 .
(2.3.)
.
(2.3.)
С другой стороны физически реализуемая цепь должна
быть устойчивой, поэтому должно выполняться условие:  < ∞.
< ∞.
Каков бы не был конкретный вид импульсной
характеристики физически реализуемой цепи всегда должен выполняться важный
принцип: выходной сигнал, отвечающий импульсному входному воздействию, не может
возникнуть до момента появления импульса на выходе, т.е. ![]() при
при ![]() < 0.
< 0.
Следовательно, возникает очень простое ограничение на вид допустимых импульсных характеристик:
![]() при
при ![]() < 0 и
< 0 и  <
∞. (3.4)
<
∞. (3.4)
Для характеристики АЛЦ используется и переходная
функция ![]() , представляющая
собой отклик цепи на воздействие, имеющее вид единичного скачка. Между
выражениями
, представляющая
собой отклик цепи на воздействие, имеющее вид единичного скачка. Между
выражениями ![]() и
и ![]() имеется следующая интегральная
связь
имеется следующая интегральная
связь
 .
(3.5.)
.
(3.5.)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.