Характеристики детерминированных сигналов. Представление произвольного сигнала в виде суммы элементарных колебаний, страница 12

Спектр  продолжим периодически на всю ось частот с периодом . Тогда для частоты в диапазоне частот от  до , функцию  можно представить в виде ряда Фурье:

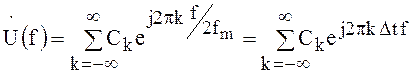, где .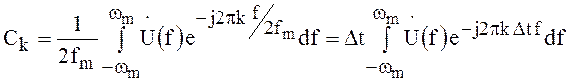

Используя выражение (119) 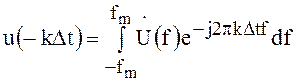, получим

, поэтому

.

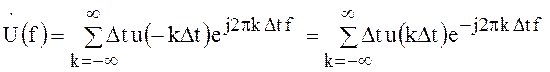Подставляя это выражение в (119), имеем

.

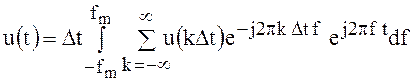Изменяя порядок выполнения операции интегрирования и суммирования, получим

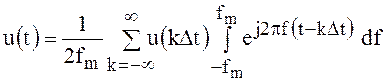, откуда следует формула (118).

Формула Котельникова даёт точную сумму для любой функции  с резко ограниченным по частоте спектром.

Восстановление непрерывного сигнала по его отсчётам. Пусть сигнал  поступает на вход идеального фильтра нижних частот с импульсной характеристикой .

Напряжение  представляет собой последовательность прямоугольных импульсов длительностью  и периодом повторения , причём площадь каждого импульса равна .

Согласно (109) отклик идеального фильтра нижних частот

.

При прохождении сигнальной импульсной последовательности через идеальный фильтр нижних частот напряжение на его выходе от k-го импульса равно

.

Напряжения на выходе фильтр нижних частот от всех импульсов

.

.

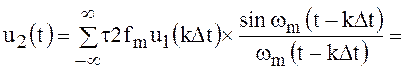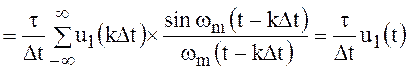Сравнивая данное выражение с формулой Котельникова, замечаем, что выходное напряжение фильтра нижних частот  отличается от его входного напряжения  лишь постоянным множителем .

Следовательно,

.

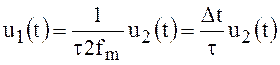Итак, сигнал , передаваемый в виде периодической последовательности прямоугольных импульсов, можно восстановить на приёмном конце линии связи, пропуская эту последовательность через фильтр нижних частот, с граничной частотой  усиливая в 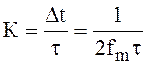 раз.

Такая схема передачи изображена на рис. 27.

0

Рис. 27

Реальные сигналы не имеют строго ограниченного спектра и, поэтому, могут передаваться по подобной линии связи с некоторыми искажениями.

Практические ограничения и их преодоления. Теорема Котельникова предполагает ограниченность частотного спектра частотой . При восстановлении сигнала по отсчётам использовался идеальный фильтр нижних частот, имеющий строго ограниченную полосу пропускания.

В реальности не существует сигналов с ограниченным спектром, так как все сигналы, ограниченные во времени, имеют бесконечную ширину спектра. Не реализуются и идеальные фильтры нижних частот, имеющие строго ограниченную полосу пропускания.

Рассмотрим влияние этих практических ограничений и способы их уменьшения их влияния. Для этого рассмотрим изменение функции  в зависимости от шага дискретизации по времени .

Процедуру дискретизации (взятие отчётов), осуществляемую с помощью электронного ключа, можно рассматривать как умножение функции  на вспомогательную функцию :

, где  - периодическая последовательность прямоугольных тактовых импульсов единичной амплитуды, имеющих длительность  и период повторения .

Периодическую функцию , полагая в формуле (96)  и ,  можно представить рядом Фурье

,            (120)

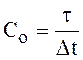где  и .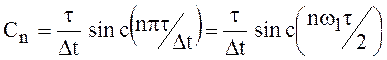

Подставляя (120) в выражение , имеем

                     (121)

Если спектром  является 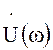, то спектр напряжения  можно представить в следующем виде:

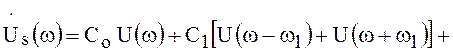
                                                      (122)

Спектры  и  изображены на рис. 28.

Рис. 28

Согласно выражению (122) коэффициенты  убывают с увеличением n, поэтому правый и левый спектры на рис. 28 должны быть меньше центрального. Однако при малой длительности отсчёта  и 1  очень мало отличается от . Поэтому на рис. 28 амплитуды спектров дискретного сигнала показаны одинаковыми.

Можно показать, что при  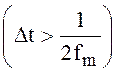спектры перекрываются. Очевидно, что сигнал  можно восстановить по спектру  с помощью фильтра нижних частот, если спектры не перекрываются, т.е. при  .

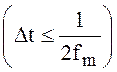Минимальная частота отсчётов  называется скоростью Найквиста. Так как реальные сигналы не имеют строго ограниченной частоты , за пределами которой спектр равен нулю, то всегда имеет место перекрытие спектров. Для уменьшения влияния перекрытия спектров можно увеличить частоту отсчётов  по сравнению с  (частота  отсчитывается на достаточно малом уровне).