Прямоугольные периодические униполярные импульсы. В радиотехнике находят широкое применение прямоугольные периодические импульсы напряжения, изображённые на рис. 1.4.

Рис. 1.4
Такие импульсы применяются, например, в радиоизмерительной
технике, телевидении и радиолокации. Длительность импульсов ![]() может измеряться
микросекундами или долями микросекунд, а иногда и долями наносекунд. Период
следования импульсов T может в сотни и тысячи раз превышать
длительность импульсов. Отношение
может измеряться
микросекундами или долями микросекунд, а иногда и долями наносекунд. Период
следования импульсов T может в сотни и тысячи раз превышать
длительность импульсов. Отношение ![]() называется
скважностью импульсов.
называется
скважностью импульсов.
Для периодической последовательности прямоугольных
импульсов напряжения имеем 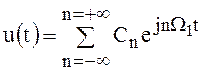 ,
,
uде  . (41)
. (41)
Здесь 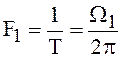 .
.
Следовательно,
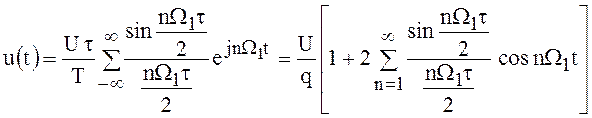 . (42)
. (42)
Амплитудный спектр импульса ![]() показан на рис. 1.5
показан на рис. 1.5

Рис. 1.5
1.4. Гармонический анализ непериодических сигналов
Интеграл Фурье. Если периодическую функцию времени можно представить рядом Фурье, состоящим из суммы гармонических составляющих, то непериодическую функцию времени можно представить интегралом Фурье при выполнении определённых условий.
Не строгим, но наглядным является представление об
интеграле Фурье как о предельной форме ряда Фурье при стремлении периода функции
Т к бесконечности. В самом деле, при увеличении периода Т расстояние вдоль оси
частот между гармониками ряда, равное ![]() , сокращается и
линейный спектр в пределе становится непрерывным.
, сокращается и
линейный спектр в пределе становится непрерывным.
Достаточным, но не необходимым условием существования
преобразования Фурье является абсолютная интегрируемость функции, т.е. конечность
интеграла  .
.
Пусть ![]() -
одиночный импульсный сигнал конечной длительности (рис. 1.6).
-
одиночный импульсный сигнал конечной длительности (рис. 1.6).

Рис. 1.6
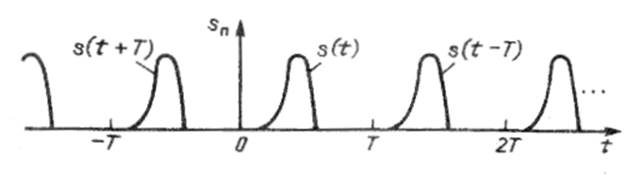
Рис. 1.7
Дополнив его мысленно такими же сигналами,
периодически следующими через некоторый интервал времени T,
получим периодическую последовательность ![]() (рис. 1.7), которая
может быть представлена в виде комплексного ряда Фурье
(рис. 1.7), которая
может быть представлена в виде комплексного ряда Фурье
 (43)
(43)
с коэффициентами
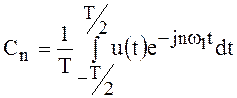 ,
где
,
где ![]() .
.
Подставив формулу коэффициента ![]() в (43), получим
в (43), получим
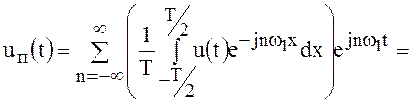
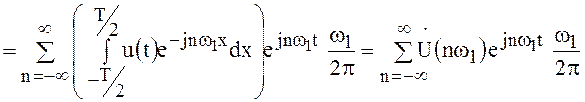 . (44)
. (44)
Для перехода от периодического сигнала ![]() к исходному непериодическому
сигналу
к исходному непериодическому
сигналу ![]() , заданному в
промежутке
, заданному в
промежутке ![]() , устремим к бесконечности
период повторения Т. Тогда расстояние между спектральными линиями спектра
, устремим к бесконечности
период повторения Т. Тогда расстояние между спектральными линиями спектра  , равное основной частоте становится бесконечно малым, т.е.
, равное основной частоте становится бесконечно малым, т.е. ![]() , но для фиксированной частоты
, но для фиксированной частоты
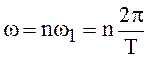 значение
значение 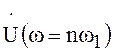 остаётся неизменным (частота фиксируется за
счёт соответствующего увеличения n при увеличении Т).
остаётся неизменным (частота фиксируется за
счёт соответствующего увеличения n при увеличении Т).
Другими словами спектр становится сплошным, поэтому можно
в выражении (44) заменить ![]() на
на
![]() ,
, ![]() на текущую частоту
на текущую частоту ![]() , а операцию суммирования
- операцией интегрирования.
, а операцию суммирования
- операцией интегрирования.
Следовательно, приходим к двойному инте6гралу Фурье
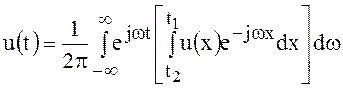 .
(45)
.
(45)
Внутренний интеграл, являющийся функцией частоты ![]() ,
,
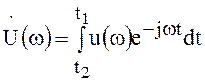 ,
(46)
,
(46)
называется спектральной плотностью или спектром функции ![]() .
.
В общем случае, когда пределы ![]() и
и ![]() не заданы, спектральная плотность записывается в
следующем виде:
не заданы, спектральная плотность записывается в
следующем виде:
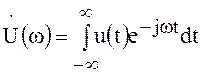 .
(47)
.
(47)
После подстановки (47) в выражение (45) получим
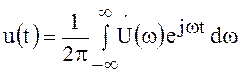 .
(48)
.
(48)
Выражения (47) и (48) называются соответственно прямым и обратным преобразованиями Фурье.
Выражения (47) и (22) отличаются только множителя ![]() . Поэтому,
спектральная плотность
. Поэтому,
спектральная плотность ![]() обладает
всеми основными свойствами коэффициентов ряда Фурье. Используя формулу Эйлера можно
написать
обладает
всеми основными свойствами коэффициентов ряда Фурье. Используя формулу Эйлера можно
написать
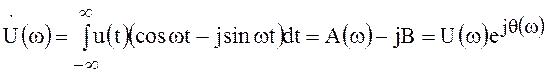 ,
(49)
,
(49)
где 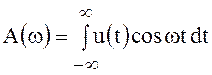 ;
;
 . (50)
. (50)
Модуль и аргумент спектральной плотности определяются выражениями
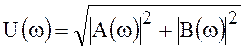 ,
(51)
,
(51)
 .
(52)
.
(52)
В формулах (51) и (52) ![]() -
амплитудно-частотная, а
-
амплитудно-частотная, а ![]() -
фазочастотная характеристики сплошного спектра непериодического колебания
-
фазочастотная характеристики сплошного спектра непериодического колебания ![]() .
.
Как и в случае ряда Фурье, ![]() является чётной, а
является чётной, а ![]() - нечётной функциями
частоты
- нечётной функциями
частоты ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.