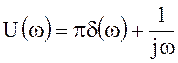Характеристики детерминированных сигналов. Представление произвольного сигнала в виде суммы элементарных колебаний, страница 8

.                                                                                  (82)

Постоянной составляющей  согласно (79) соответствует спектр , а нечётной функции 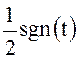 - мнимое значение спектра .

Прямоугольный импульс. Рассмотрим случай, когда сигнал представляет собой одинокий прямоугольный импульс, расположенный симметрично относительно начала отсчёта времени (рис.15).

Рис. 15

Если амплитуда импульса равна U, а длительность , то такой импульс описывается выражением:

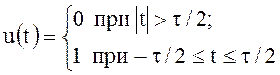.                                                                (83)

В соответствии с (47) спектр прямоугольного импульса

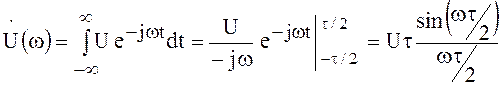.                          (84)

Заметим, что произведение , равное площади импульса, определяет значение спектра при , т.е. 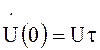 (см. рис. 15).

Таким образом, выражение (84) можно записать в следующем виде:

,                                                  (85)

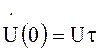где  и .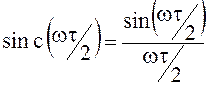

Функция , определяющая спектр прямоугольного импульса, изображена на рис. 16.

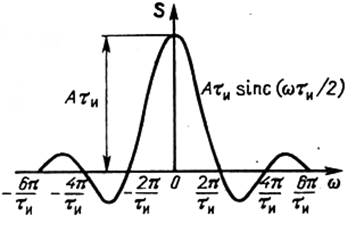
Рис. 16

Колокольный импульс.Представленный на рис. 17, колокольный (гауссовский) импульс определяется следующим выражением:

.                                                                                      (86)

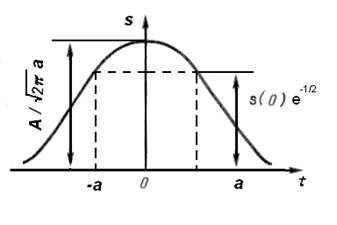
Рис. 17

Спектр такого импульса

.

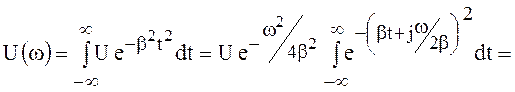
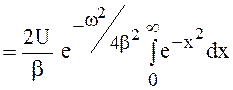Учитывая, что интеграл в правой части равен , находим

.                                                                           (87)

Рассмотрим вопрос соотношения длительности сигнала с шириной его спектра на примере колокольного импульса. Положим, что .

Величину  можно назвать длительностью импульса на уровне , так как при  высота импульса падает в e раз. В этом случае выражение () для спектра примет вид

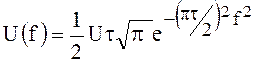,                                                                    (88)

откуда следует, что ширина спектра на уровне

при одностороннем отсчёте равна

 и 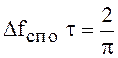.                                                                                      (89)

Можно показать, что любого импульсного сигнала это произведение является постоянной величиной, т.е. .                             (90)

Из выражения (90) следует важный вывод: невозможно одновременно сконцентрировать сигнал в узкой полосе частот и в коротком интервале времени.

1.7. Соотношение между длительностью сигнала и шириной его спектра

Из результатов анализа сигналов различной формы следует, что чем меньше длительность сигнала, тем шире его спектр и наоборот.

Основным результатом исследования является то, что значение произведения  при фиксированном значении энергетической эффективности  максимально для прямоугольного импульса и минимально для колокольного. В частности, уровню % для прямоугольного, треугольного и колокольного импульсов соответствуют значения , равные 1,8; 0,94; и 0,48.

Отметим, что в некоторых практических задачах для точного сохранения формы исходного сигнала произведение  должно быть значительно больше единицы.

В любом случае при заданной форме сигнала сжатие его во времени с целью, например, повышения точности определения момента его появления неизбежно сопровождается расширением спектра, что заставляет расширять полосу пропускания устройства обработки сигналов. Аналогично сжатие спектра импульса с целью повышения точности измерения частоты неизбежно сопровождается растяжением сигнала во времени, что требует увеличения времени наблюдения (обработки).

1.8. Корреляционные функции

Одним из важных функции, расширяющих представления о сигналах и их свойствах, является автокорреляционная и взаимно корреляционная функций.

Корреляционная функция для вещественного сигнала  по определению равна

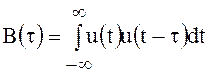,                                                                          (91)

где  - временной сдвиг.

При нулевом временном сдвиге  имеем

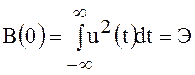,                                                                             (92)

где Э – энергия сигнала. Следовательно, при нулевом временном сдвиге автокорреляционная функция равна энергии сигнала.

Перечислим основные свойства автокорреляционной функции: