Характеристики детерминированных сигналов. Представление произвольного сигнала в виде суммы элементарных колебаний, страница 14

Тогда при проведении дуги в левой полуплоскости, т.е. при  (рис. 30 a), контур интегрирования охватывает все полюсы подынтегральной функции, лежащие левее прямой , интеграл (125) превращается в контурный интеграл, и в соответствии с теоремой о вычетах получим выражение

,                                          (126)

где  - вычет в полюсе k подынтегральной функции.

а/                                                              б/

Рис. 30

Таким образом, вычисление интеграла в выражении (126) сводится к определению вычетов в полюсах подынтегральной функции. Представим подынтегральную функцию выражения () в виде отношения полиномов

.

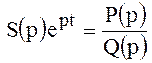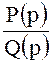Полюсы подынтегральной функции определяются из условия равенства нулю её знаменателя . Тогда вычет функции , имеющий в точке  простой полюс первой кратности, определяется формулой

.                                                                  (127)

При проведении дуги в правой полуплоскости, т.е. при t < 0 (рис. 30б), полюсы подынтегральной функции оказываются вне контура интегрирования  и в соответствии с теоремой Коши интеграл по замкнутому контуру равен нулю:

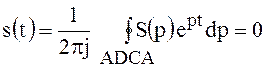.                                                                 (128)

Глава 2

РАДИОСИГНАЛЫ

Радиосигнал получается в модуляционном устройстве (рис. 1.), на которое одновременно поступают высокочастотное колебание, создаваемое автогенератором, и управляющий сигнал.

Рис. 1

Высокочастотное колебание, формируемое автогенератором, имеет вид гармонического колебания

 

и характеризуется тремя параметрами: амплитудой , угловой (круговой) частотой  и начальной фазой. Отображение управляющего сигнала в высокочастотном колебании, создаваемом автогенератором, состоит в изменении амплитуды, частоты и фазы высокочастотного колебания по закону управляющего сигнала. В зависимости от того, какой из указанных параметров высокочастотного колебания изменяется по закону управляющего сигнала, различают амплитудную, частотную и фазовую модуляции:

при амплитудной модуляции (АМ)

;

при частотной модуляции (ЧМ)

;

при фазовой модуляции (ФМ)

,

причём функции ,  и  повторяют управляющий (модулирующий) сигнал :

;

;

.

В простейшем случае модулирующий сигнал является косинусоидальным: , причём  « . Частота  называется несущей.

1.1. Радиосигналы с амплитудной модуляцией

Однотональные радиосигналы с амплитудной модуляцией

При амплитудной модуляции изменение амплитуды высокочастотного колебания пропорционально управляющему сигналу

, а сам АМ радиосигнал .       ()

Здесь 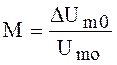 - коэффициент амплитудной модуляции, величина пропорциональная амплитуде управляющего напряжения. Обычно ; частный случай  соответствует отсутствию модуляции.

Осциллограммы модулирующего напряжения  и АМ напряжения  изображены на рис. 2.

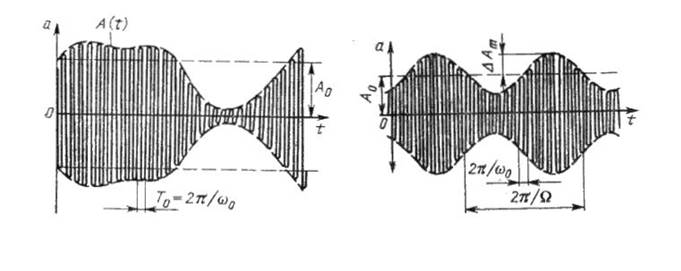
Рис. 2

Спектральное разложение однотонального АМ радиосигнала. Полагая  и преобразуя произведение косинусов в сумму, представим выражение () в следующем виде:

.           ()

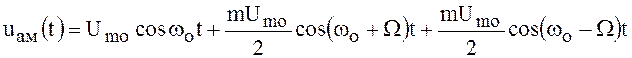Выражение АМ радиосигнала содержит три частотные составляющие: первая частотная составляющая – основная, а две другие боковые.

Спектры модулирующего сигнала и АМ радиосигнала изображены на рис. 3. Откуда видно, что ширина спектра АМ радиосигнала в два раза больше ширины спектра модулирующего сигнала, т.е. .

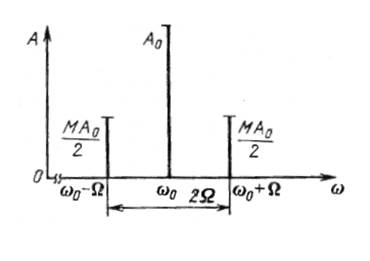
Рис. 3

Векторная диаграмма однотонального АМ радиосигнала.Каждую составляющую АМ радиосигнала можно интерпретировать как проекцию на неподвижную ось (вертикаль) вектора, равномерно вращающегося в направлении против часовой стрелки. Величина этого вектора равна амплитуде составляющей, а угловая скорость вращения – её круговой частоте. Взаимное расположение этих векторов для двух различных моментов времени показано на рис. 4.

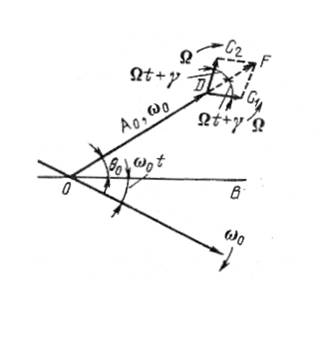
Рис. 4

Интересуясь взаимным расположением вращающихся векторов, будем полагать один из векторов, а именно вектор основной составляющей 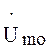, неподвижным (точнее – будем считать показанную на рис. 4, ось проекции ОА, вращающейся со скоростью  по часовой стрелке).