В данном случае спектр АМ колебания содержит три составляющие, поэтому структуру колебания на выходе усилителя можно выявить, рассматривая прохождение через усилитель каждой из составляющих отдельно.
Записав выражение () в форме
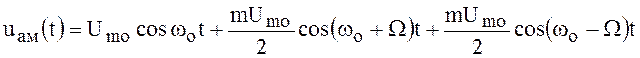 , ()
, ()
найдём передаточные функции
резонансного усилителя для частот ![]() ,
, ![]() и
и
![]()
Для выражения передаточной функции резонансного усилителя имеем
 ,
(3. )
,
(3. )
где ![]() - резонансный
коэффициент усиления;
- резонансный
коэффициент усиления; 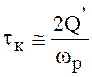 - постоянная
времени контура.
- постоянная
времени контура.
Основываясь на выражении () и положив ![]() и
и ![]() , имеем:
, имеем:
![]() ;
;
для составляющей
верхней боковой частоты ![]()
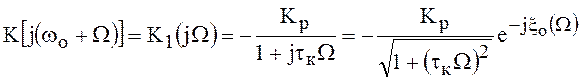 ;
;
для составляющей
нижней боковой частоты ![]()
 , где
, где ![]() - фазовый сдвиг в контуре на боковых частотах
(запаздывание на верхней и опережение на нижней боковых частотах).
- фазовый сдвиг в контуре на боковых частотах
(запаздывание на верхней и опережение на нижней боковых частотах).
С учётом амплитудных и фазовых изменении спектральных составляющих в резонансном усилителе, можно представить выходное напряжение, аналогичной ():
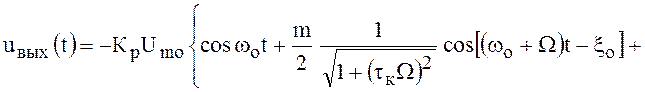
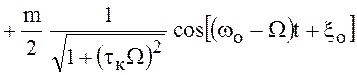 .
.
Свернув это выражение, получим
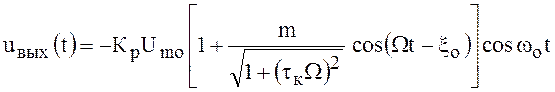 .
()
.
()
Сравним полученное выражение с (). Как следовало
ожидать, частота и фаза АМ напряжения при прохождении через резонансный
усилитель ![]() не изменяются.
не изменяются.
Инерционность колебательного контура оказывает влияние на огибающую выходного напряжения:
1/ глубина модуляции на выходе
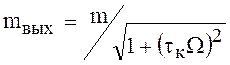
меньше, чем на входе; относительное уменьшение глубины модуляции, иногда называемое коэффициентом демодуляции,
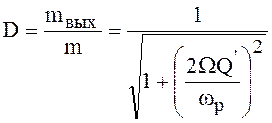
(график зависимости D от частоты модуляции Ω, представленный на рис. , соответствует правой ветви резонансной кривой колебательного контура);
2/ огибающая амплитуд на выходе усилителя отстаёт по фазе от огибающей
входного напряжения на угол 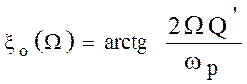 .
.
Рис.
Зависимости ![]() и
и
![]() от частоты модуляции
от частоты модуляции ![]() обусловлены тем, что
инерционность контура снижает скорость изменения во времени огибающей
колебания. При этом, однако форма огибающей остаётся неизменной.
обусловлены тем, что
инерционность контура снижает скорость изменения во времени огибающей
колебания. При этом, однако форма огибающей остаётся неизменной.
Зависимость коэффициента демодуляции от частоты
модуляции приведена на рис. , из которой следует, что чем больше частота модуляции
![]() , тем больше
относительное ослабление амплитуды колебаний боковых частот и, следовательно,
меньше глубина модуляции колебаний. Смысл полученного результата поясняется
рис. , на котором показано относительное положение спектра входного напряжения
относительно резонансной кривой контура усилителя.
, тем больше
относительное ослабление амплитуды колебаний боковых частот и, следовательно,
меньше глубина модуляции колебаний. Смысл полученного результата поясняется
рис. , на котором показано относительное положение спектра входного напряжения
относительно резонансной кривой контура усилителя.
a/ b/
Рис.
Результаты анализа тональной модуляции позволяют
представить общую картину изменений при прохождении через резонансный усилитель
напряжения, модулированного по амплитуде сложным сигналом. Входящим в такой
сигнал различным частотам модуляции ![]() соответствует
неодинаковое ослабление: чем выше частота модуляции, тем сильнее выражена
демодуляция. Поскольку при приёме АМ колебаний напряжение на выходе детектора
приёмника пропорционально коэффициенту модуляции, получается относительное
ослабление составляющих высших частот модуляции. Следовательно, зависимость
соответствует
неодинаковое ослабление: чем выше частота модуляции, тем сильнее выражена
демодуляция. Поскольку при приёме АМ колебаний напряжение на выходе детектора
приёмника пропорционально коэффициенту модуляции, получается относительное
ослабление составляющих высших частот модуляции. Следовательно, зависимость ![]() определяет степень
линейных частотных искажений передаваемого сигнала. Эти искажения называются
линейными потому, что они не сопровождаются возникновением новых частотных
составляющих.
определяет степень
линейных частотных искажений передаваемого сигнала. Эти искажения называются
линейными потому, что они не сопровождаются возникновением новых частотных
составляющих.
Имеет место также задержка сигнала. Это обусловлено тем, что фазовый сдвиг огибающей (при тональной модуляции) зависит от частоты модуляции. Контур оказывает влияние на сигнал, содержащийся в огибающей, так же как фильтр нижних частот при прохождении через него сигнала.
Задержка определяется наклоном ФЧХ контура в точке ![]() :
:
 .
.
Как правило, задержку определяют пол наклону ФЧХ в
точке ![]() , тогда
, тогда 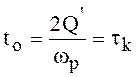 .
.
Следовательно, задержка сигнала в одиночном контуре, полоса пропускания которого достаточна для удовлетворительного прохождения спектра сигнала, равна постоянной времени контура.
Пусть контур усилителя неточно настроен на несущую
частоту ![]() АМ напряжения (рис.
). .Частотная расстрой-ка контура приводит к асимметрии составляющих боковых
частот на выходе резонансного усилителя. Причина возникновения асимметрии
поясняется векторной диаграммой на рис. . На этой диаграмме вектор ОД
изображает несущее напряжение. Амплитуда напряжения верхней боковой частоты
(вектор
АМ напряжения (рис.
). .Частотная расстрой-ка контура приводит к асимметрии составляющих боковых
частот на выходе резонансного усилителя. Причина возникновения асимметрии
поясняется векторной диаграммой на рис. . На этой диаграмме вектор ОД
изображает несущее напряжение. Амплитуда напряжения верхней боковой частоты
(вектор ![]() ) в данном случае (
) в данном случае (![]() ) значительно меньше
амплитуды напряжения нижней боковой частоты (вектор
) значительно меньше
амплитуды напряжения нижней боковой частоты (вектор ![]() ). Длина равнодействующего
вектора OF, изображающего результирующее напряжение, изменяется
по сложному закону, не совпадающему с гармоническим законом изменения огибающей
входного напряжения.
). Длина равнодействующего
вектора OF, изображающего результирующее напряжение, изменяется
по сложному закону, не совпадающему с гармоническим законом изменения огибающей
входного напряжения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.