Характеристики детерминированных сигналов. Представление произвольного сигнала в виде суммы элементарных колебаний, страница 17

2.2. Радиосигналы с угловой модуляцией

Выражение немодулированного колебания представим в следующем виде:

. Здесь,  и  - амплитуда, угловая частота и начальная фаза являются постоянными величинами;  - полная фаза колебания.

Набег фаза за какой-либо конечный промежуток времени  равен

.                                (1)

Отсюда видно, при постоянной угловой частоте  набег фазы за какой-либо промежуток времени пропорционален длительности этого промежутка. С другой стороны, если известно, что набег фазы за время , равен , то угловую частоту можно определить как отношение

.                                                                                  (2)

При этом в течение рассматриваемого промежутка времени частота сохраняет постоянное значение. Из выражения (2) видно, что угловая частота есть не что иное, как скорость изменения фазы колебания.

Переходя к колебанию, частота которого может изменяться во времени, равенства (1) и (2) необходимо заменить интегральным и дифференциальным соотношениями:

,                                                                          (3)

.                                                                                              (4)

На основании выражений (3) и (4) полную фазу высокочастотного колебания в момент времени t можно записать так

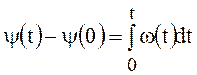 или , где .

Общее выражение высокочастотного колебания, амплитуда которого постоянна т.е. , а угловая частота модулирована, можно представить в следующем ви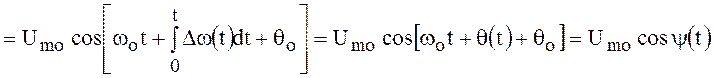де:

, где ; .

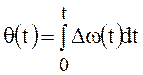Мгновенная частота высокочастотного колебания равна

.

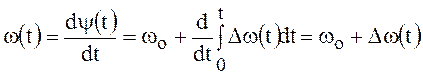Мгновенная частота изменяется около частоты , причём отклонение частоты  « .

Фазомодулированное колебание. При фазовой модуляции  и полная фаза колебания  связана с модулирующим сигналом  зависимостью , где  и  - значение угловой частоты и начальной фазы колебания в отсутствие модуляции;  - постоянный коэффициент пропорциональности.

Тогда выражение ФМ радиосигнала можно представить в следующем виде:

.                                                     ()

Если модулирующий сигнал , то  является гармоническим колебанием.

Фазовый сдвиг между полными фазами ФМ радиосигнала и немодулированного колебания , а максимальный фазовый сдвиг, называемый девиацией фазы равен .

Так как выражение мгновенной частоты ФМ радиосигнала равна 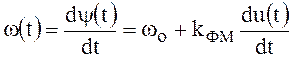, то процесс фазовой модуляции всегда сопровождается частотной модуляцией.

Частотно-модулированное колебание. При частотной модуляции между мгновенной частотой и модулирующим сигналом  имеется связь .

Поэтому полная фаза ЧМ колебания записывается в виде:

.

Поэтому выражение ЧМ радиосигнала можно представить в следующем виде:

.                                        ()

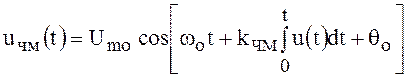Частотный сдвиг между ФМ радиосигналом и немодулированным колебанием составляет , а максимальный частотный сдвиг, называемый девиацией частоты, равен .

Процесс частотной модуляции всегда сопровождается фазовой модуляцией, так как возникает составляющая фазы, обусловленная модулирующим сигналом .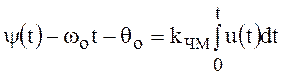

Если функция модулирующего сигнала  является достаточно гладкой, то внешне осциллограммы ФМ и ЧМ колебаний не отличаются. Однако, имеется принципиальная разница: фазовый сдвиг между ФМ радиосигналом и немодулированным колебанием пропорционален , в то время как для ЧМ радиосигнала этот сдвиг пропорционален интегралу от передаваемого сигнала .

Однотональные радиосигналы с угловой модуляцией

Анализ ФМ и ЧМ радиосигналов с математической точки зрения гораздо сложнее, чем анализ АМ радиосигнала. Поэтому с целью изучения основных закономерностей основное внимание будем уделять простейшим однотональным ФМ и ЧМ радиосигналам.

Однотональный ЧМ радиосигнал. В этом случае модулирующий сигнал представим в виде . Тогда для выражения мгновенной частоты имеем:

, где . Девиация частоты пропорциональна только амплитуде модулирующего сигнала .

Полная фаза ЧМ радиосигнала

, где  - индекс модуляции.

Индекс модуляции прямо пропорционален амплитуде  и обратно пропорционален частоте  модулирующего сигнала.