С помощью выражения (48) легко получить тригонометрическую форму преобразования Фурье:
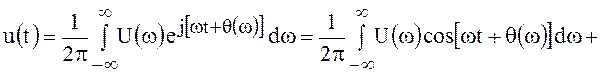
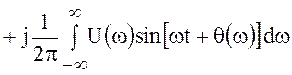 .
.
Из чётности модуля и нечётности фазы следует, что
подынтегральная функция в первом интеграле является чётной, а во втором –
нечётной относительно ![]() .
Следовательно, второй интеграл равен нулю, и окончательно получим
.
Следовательно, второй интеграл равен нулю, и окончательно получим
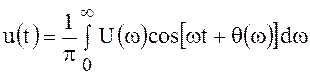 .
(53)
.
(53)
Переход от комплексной формы (48) к тригонометрической (53) целесообразен в конце анализа. Все промежуточные расчёты при применении интеграла Фурье удобнее и проще проводить на основании комплексной формы (53).
Проведём сравнение спектров периодической последовательности импульсов и одиночного импульса этой последовательности (рис. 1.6 и рис. 1.7). Для этого рассмотрим выражение (44), из которого следует
 .
(54)
.
(54)
Здесь  - значение
спектральной плотности одиночного импульса на частоте
- значение
спектральной плотности одиночного импульса на частоте ![]() , а
, а ![]() - частота следования
импульсов.
- частота следования
импульсов.
Комплексная амплитуда n-й гармоники спектра периодического сигнала
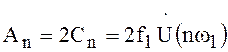 .
(55)
.
(55)
Следовательно, модуль спектральной плотности одиночного импульса и огибающая дискретного спектра периодической последовательности импульсов, полученной путём повторения заданного импульса, совпадают по форме и отличаются лишь масштабом. Это свойство позволяет найти коэффициенты ряда Фурье по спектральной плотности одиночного импульса с помощью формулы (2.58).
Модуль спектральной плотности одиночного импульса и дискретный (линейчатый) спектр периодической последовательности этих же импульсов приведены на рис. 1.8 и рис. 1.9.
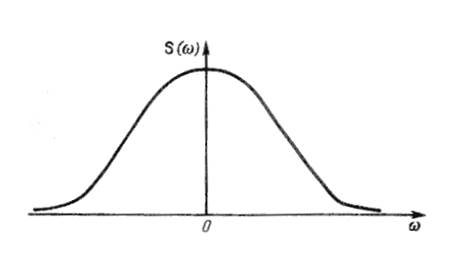
Рис. 1.8
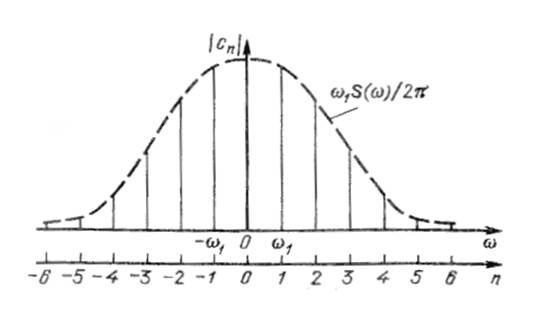
Рис. 1.9
На этом рисунке огибающая дискретного спектра  изображена штриховой
линией.
изображена штриховой
линией.
С увеличением периода Т спектральные линии на рис. 10
сближаются и коэффициенты ряда ![]() уменьшаются,
так, что отношение
уменьшаются,
так, что отношение ![]() остаётся
постоянным. В пределе, когда
остаётся
постоянным. В пределе, когда ![]() приходим
к одиночному импульсу со спектральной плотностью
приходим
к одиночному импульсу со спектральной плотностью
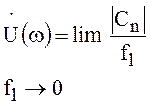 .
(56)
.
(56)
Из полученного выражения следует, что спектральная
плотность  - амплитуда
напряжения (тока), приходящаяся на 1 Гц в бесконечной узкой полосе частот,
которая включает в себя рассматриваемую частоту
- амплитуда
напряжения (тока), приходящаяся на 1 Гц в бесконечной узкой полосе частот,
которая включает в себя рассматриваемую частоту ![]() .
.
1.4.Основные свойства преобразований Фурье
Формулы прямого и обратного преобразований Фурье устанавливают
однозначное соответствие между сигналом ![]() и его спектром
и его спектром  . Основные свойства
преобразований Фурье, рассматриваемые ниже, позволяют получить исчерпывающее
представление об этом соответствии и облегчают использование спектральных
преобразований при решении практических задач.
. Основные свойства
преобразований Фурье, рассматриваемые ниже, позволяют получить исчерпывающее
представление об этом соответствии и облегчают использование спектральных
преобразований при решении практических задач.
Сдвиг сигнала во времени. Пусть сигнал ![]() (рис. 1.10), обладающий
спектром
(рис. 1.10), обладающий
спектром 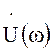 , задержан на время
, задержан на время ![]() (при сохранении его
формы).
(при сохранении его
формы).
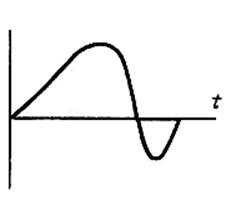
Рис. 1.10
Спектр задержанного сигнала ![]()
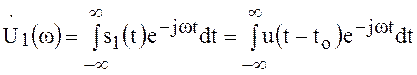 .
.
Вводя новую переменную интегрирования ![]() , получаем
, получаем
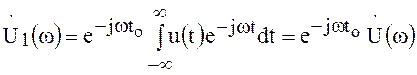 .
(57)
.
(57)
Таким образом, сдвиг сигнала по времени на ![]() эквивалентен изменению
фазового сдвига составляющих спектра на величину
эквивалентен изменению
фазового сдвига составляющих спектра на величину ![]() .
.
Справедливо и обратное утверждение: дополнительный
сдвиг всех составляющих спектра на величину ![]() эквивалентен
запаздыванию сигнала на время.
эквивалентен
запаздыванию сигнала на время.
Изменение масштаба времени. Пусть сигнал ![]() со спектром
со спектром  подвергся сжатию во времени (рис. 1.11). Новый
сжатый сигнал
подвергся сжатию во времени (рис. 1.11). Новый
сжатый сигнал ![]() (штриховая кривая на рис .11) связан с исходным
сигналом соотношением
(штриховая кривая на рис .11) связан с исходным
сигналом соотношением ![]() ,где
,где ![]() > 1. (58)
> 1. (58)
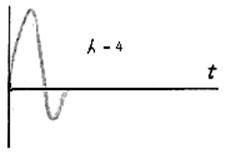
Рис. 1.11
Умножение времени t на постоянный коэффициент ![]() эквивалентно
изменению масштаба времени.
эквивалентно
изменению масштаба времени.
Следовательно, функция ![]() принимает те же
значения, что и функция
принимает те же
значения, что и функция ![]() ,
но в более ранние или поздние моменты времени.
,
но в более ранние или поздние моменты времени.
Спектр такого сигнала
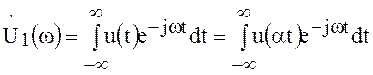 .
.
Вводя новую переменную интегрирования ![]() , получаем
, получаем
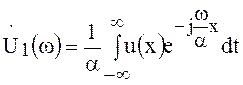 .
.
Но интеграл в правой части этого выражения есть не что
иное, как спектр функции ![]() при
частоте
при
частоте ![]() , т.е.
, т.е. 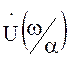 . Таким образом,
. Таким образом,
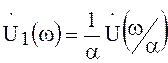 .
(59)
.
(59)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.