Векторы боковых составляющих 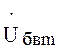 и
и 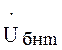 вращаются навстречу друг другу со скоростью
вращаются навстречу друг другу со скоростью ![]() относительно неподвижного вектора
относительно неподвижного вектора 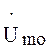 . Поскольку векторы
. Поскольку векторы 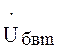 и
и  имеют одинаковую
длину и вращаются с одинаковой по абсолютной величине скоростью навстречу друг
другу, их сумма
имеют одинаковую
длину и вращаются с одинаковой по абсолютной величине скоростью навстречу друг
другу, их сумма  будет
представлять собой вектор, коллинеарный вектору
будет
представлять собой вектор, коллинеарный вектору 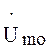 (рис. 4.). Вектор
(рис. 4.). Вектор 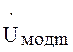 существует только
при наличии модуляции
существует только
при наличии модуляции ![]() , поэтому он называется модуляционным вектором.
Оставаясь коллинеарным вектору
, поэтому он называется модуляционным вектором.
Оставаясь коллинеарным вектору 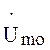 ,
он меняет свою длину и направление в соответствии с управляющим сигналом,
причём амплитуда модуляционного вектора
,
он меняет свою длину и направление в соответствии с управляющим сигналом,
причём амплитуда модуляционного вектора ![]() .
.
Следовательно, рассмотренное АМ колебание,
представляющее сумму гармонических колебаний (с частотами ![]() и
и ![]() ), можно рассматривать
как высокочастотное колебания с частотой
), можно рассматривать
как высокочастотное колебания с частотой ![]() , амплитуда которого
изменяется по закону
, амплитуда которого
изменяется по закону ![]() , где величина
, где величина ![]() пропорциональна
мгновенному значению модулирующего напряжения.
пропорциональна
мгновенному значению модулирующего напряжения.
Мощность АМ радиосигнала. Определим среднюю мощность АМ колебания () за длительный интервал времени. Поскольку это колебание является суммой трёх гармонических составляющих, среднюю мощность, выделяемую в сопротивлении нагрузки R, можно определить, как сумму средних мощностей, выделяемых каждой частотной составляющей.
В отсутствие модулирующего сигнала (m=0) антенна
передатчика эквивалентна активному сопротивлению R, питается
косинусоидальным током ![]() и
потребляет от передатчика мощность
и
потребляет от передатчика мощность
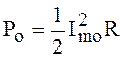 .
()
.
()
Величина ![]() называется мощностью передатчика в режиме
молчания (в режиме несущей частоты). Сравним с нею мощности, составляющих АМ
колебания, когда АМ ток выражается соотношением
называется мощностью передатчика в режиме
молчания (в режиме несущей частоты). Сравним с нею мощности, составляющих АМ
колебания, когда АМ ток выражается соотношением
![]()
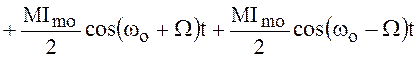 .
.
Найдём среднюю мощность ![]() за период
за период 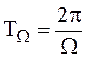 колебания низкой
частоты, так называемую телефонную мощность модулированного колебания.
Её можно определить как сумму средних за период
колебания низкой
частоты, так называемую телефонную мощность модулированного колебания.
Её можно определить как сумму средних за период ![]() мощностей каждой из
гармонических составляющих тока
мощностей каждой из
гармонических составляющих тока ![]()
 или, используя равенство
или, используя равенство
(), получим  .
()
.
()
Из формулы () следует, что телефонная мощность больше мощности в режиме молчания и может превосходить её в 1, 5 раза (при m=1).
Обратимся теперь к средней мощности ![]() за период высокочастотного АМ колебания
за период высокочастотного АМ колебания  . Поскольку амплитуда такого колебания непостоянна,
то и величина
. Поскольку амплитуда такого колебания непостоянна,
то и величина ![]() будет
также непостоянна. Максимальное значение она будет иметь для того периода
высокочастотного колебания, который соответствует максимальной амплитуде
высокочастотного колебания:
будет
также непостоянна. Максимальное значение она будет иметь для того периода
высокочастотного колебания, который соответствует максимальной амплитуде
высокочастотного колебания:
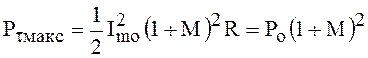 .
(a)
.
(a)
Для периода высокочастотного колебания с наименьшей амплитудой рассматриваемая мощность минимальна:
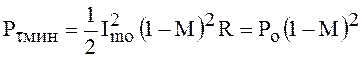 .
()
.
()
В частном случае при m=1 ![]() и
и ![]() .
.
Следовательно, при АМ выходной каскад передатчика отдаёт в нагрузку (антенну) четырёхкратную мощность по сравнению с мощностью в режиме молчания. В соответствии с этим выбирается электронный прибор выходного каскада передатчика. Однако её номинальная мощность используется далеко не полностью, особенно при малых значениях m, когда средняя мощность близка к мощности в режиме молчания. В этом заключается существенный недостаток амплитудной модуляции.
АМ радиосигналы при модуляции сложным сигналом
Сходные результаты получаются при амплитудной модуляции более сложным сигналом.
Пусть управляющий сигнал состоит из суммы
гармонических колебаний различных частот 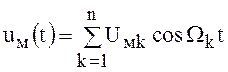 .
()
.
()
Тогда амплитуда АМ колебания будет равна
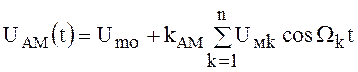 ,
а выражение АМ радиосигнала можно представить в следующем виде:
,
а выражение АМ радиосигнала можно представить в следующем виде:
 .
()
.
()
Величины 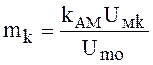 ,
называемые парциальными коэффициентами модуляции, представляют собой
коэффициенты модуляции амплитуды соответствующими составляющими управляющего
сигнала. Коэффициенты
,
называемые парциальными коэффициентами модуляции, представляют собой
коэффициенты модуляции амплитуды соответствующими составляющими управляющего
сигнала. Коэффициенты ![]() пропорциональны соответствующим амплитудам
пропорциональны соответствующим амплитудам ![]() . Для определения спектра рассматриваемого
колебания перепишем () в виде
. Для определения спектра рассматриваемого
колебания перепишем () в виде
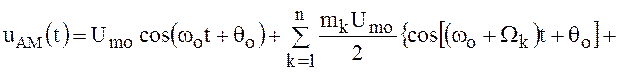
![]() .
()
.
()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.