Таким образом, уменьшение длительности импульса любой
формы в ![]() раз сопровождается
расширением его спектра во столько же раз и наоборот. Модуль спектральной
плотности при этом уменьшается в
раз сопровождается
расширением его спектра во столько же раз и наоборот. Модуль спектральной
плотности при этом уменьшается в ![]() раз
и наоборот.
раз
и наоборот.
Взаимная обратимость частоты и времени. Обращаясь формулам (47) и (48), определяющим прямое и обратное преобразования Фурье, замечаем, что они обладают существенной симметрией.
Запишем преобразования Фурье в строго симметричной форме:
 и
и 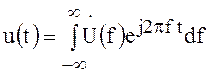 .
.
Заменяя f на t, а t на f в выражении ![]() , получаем
, получаем
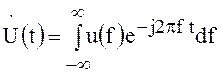 , что эквивалентно выражению
, что эквивалентно выражению ![]() ,
за исключением знака в показателе экспоненты.
,
за исключением знака в показателе экспоненты.
На этом основании приходим к следующему виду: если
сигнал ![]() имеет спектр
имеет спектр ![]() , то сигналу
, то сигналу ![]() соответствует спектр
соответствует спектр
![]() .
.
Сложение сигналов и спектров. Из линейности прямого преобразования Фурье следует, что сигнал
![]() ,
(60)
,
(60)
являющийся суммой сигналов, имеет спектр
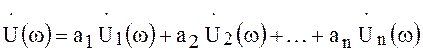 .
(61)
.
(61)
Умножение сигналов и спектров. Пусть рассматриваемый сигнал является свёрткой двух сигналов:
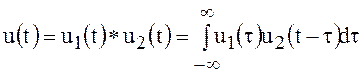 . (62)
. (62)
Спектр такого сигнала
 .
.
Изменив порядок интегрирования, получим
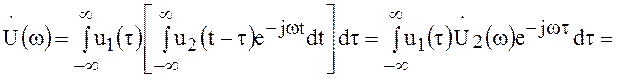
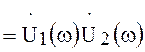 .
(63)
.
(63)
Следовательно, спектр свёртки двух сигналов равен произведению их спектров.
Вследствие взаимной обратимости частоты и времени спектр сигнала, равный произведению двух сигналов
![]() ,
(64)
,
(64)
представляет собой свёртку их спектров
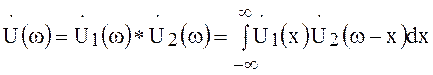 .
(65)
.
(65)
Дифференцирование и интегрирование. Пусть 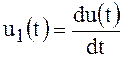 , тогда
, тогда
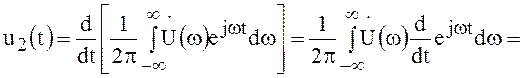
 , откуда
, откуда 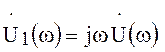 .
(66)
.
(66)
Итак, дифференцирование сигнала эквивалентно умножению
его спектра на величину ![]() .
При дифференцировании подчёркиваются (увеличиваются) высокочастотные
составляющие спектра сигнала.
.
При дифференцировании подчёркиваются (увеличиваются) высокочастотные
составляющие спектра сигнала.
Пусть 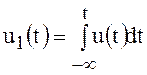 ,
тогда
,
тогда 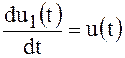 .
.
Используя, выражение (66) имеем
 ,
,
откуда 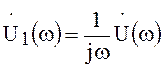 .
(67)
.
(67)
Следовательно, интегрирование сигнала эквивалентно
делению его спектра на величину ![]() .
При интегрировании высокочастотные составляющие спектра сигнала ослабляются в
большей степени, чем низкочастотные.
.
При интегрировании высокочастотные составляющие спектра сигнала ослабляются в
большей степени, чем низкочастотные.
Необходимо, отметить, что в отличие от операции
дифференцирования операция интегрирования законна только для сигналов, удовлетворяющих
условию 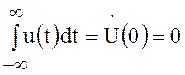 , т.е. для сигналов с
нулевой площадью.
, т.е. для сигналов с
нулевой площадью.
1.5. Энергетический спектр и спектр мощности непериодического сигнала.
Представление об энергетическом спектре
непериодического сигнала связано с энергией Э, выделяющейся в сопротивлении
1Ом, на котором действует напряжение сигнала ![]() .
.
Энергия сигнала
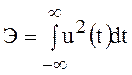 .
(68)
.
(68)
Этот интеграл конечен, в частности, для сигналов, заданных на конечном интервале времени. Для сигналов, не обращающихся в нуль на бесконечности, интеграл расходится и энергия бесконечно велика. Поэтому применительно к сигналам говорят не об энергии, а о мощности, энергии, рассеиваемой в единицу времени.
Используя прямое и обратное преобразования Фурье (47) и (48), энергию сигнала можно записать в следующем виде:
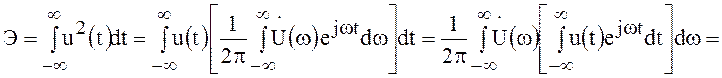
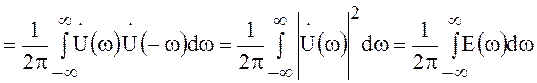 . (69)
. (69)
Здесь 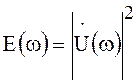 -
энергетический спектр сигнала конечной длительности. Её значение на частоте
-
энергетический спектр сигнала конечной длительности. Её значение на частоте ![]() равно энергии
сигнала, приходящейся на полосу в 1 Гц, вблизи частоты
равно энергии
сигнала, приходящейся на полосу в 1 Гц, вблизи частоты ![]() .
.
Соотношение (69) называется равенством Парсеваля. Оно
утверждает, что энергия, содержащаяся в сигнале ![]() , равна сумме энергий
всех составляющих его спектра.
, равна сумме энергий
всех составляющих его спектра.
Соотношение, аналогичное (69), можно написать и для мощности сигнала Р:
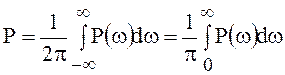 ,
(70)
,
(70)
где ![]() - спектр мощности
сигнала.
- спектр мощности
сигнала.
Мощность непериодического сигнала, не удовлетворяющего условию абсолютной интегрируемости, можно определить как
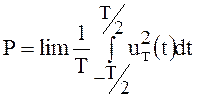 .
.
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.