Выражение однотонального ЧМ радиосигнала на основании
формулы полной фазы ![]() можно
записать в следующем виде:
можно
записать в следующем виде:
![]() .
()
.
()
Осциллограммы модулирующего сигнала и ЧМ радиосигнала изображены на рис. .
Рис. 10
Однотональный ФМ радиосигнал. В случае ФМ радиосигнала полная фаза колебания запишется так
![]() , где
, где ![]() - девиация фазы,
прямо пропорциональна амплитуде модулирующего сигнала. При этом мгновенная
частота ФМ радиосигнала равна
- девиация фазы,
прямо пропорциональна амплитуде модулирующего сигнала. При этом мгновенная
частота ФМ радиосигнала равна 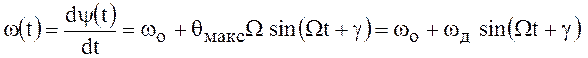 ,
где
,
где
![]() - девиация частоты, прямо пропорциональна
амплитуде
- девиация частоты, прямо пропорциональна
амплитуде ![]() и частоте
и частоте ![]() модулирующего
сигнала.
модулирующего
сигнала.
Выражение однотонального ЧМ радиосигнала на основании
формулы полной фазы ![]() можно
записать в следующем виде:
можно
записать в следующем виде:
![]() .
()
.
()
Осциллограммы модулирующего сигнала и ФМ радиосигнала изображены на рис. 11.
Рис. 11
Спектральное разложение ЧМ и ФМ радиосигналов при малых значения индексах модуляции. Спектральный анализ ЧМ и ФМ радиосигналов проведём воспользовавшись выражением однотональной угловой модуляции, записанной в следующем виде:
![]()
![]()
![]() . ()
. ()
Так как индекс угловой модуляции мал m « 1,
то можно пользоваться приближёнными равенствами ![]() и
и ![]() .
.
Тогда выражение отнотонального ЧМ (ФМ) радиосигнала запишется так
![]()
 .
()
.
()
В спектре радиосигнала с угловой модуляцией при m «
1 содержатся несущее колебание с частотой ![]() и две боковые
составляющие с частотами
и две боковые
составляющие с частотами ![]() и
и
![]() . Индекс угловой
модуляции m играет такую же роль, как коэффициент амплитудной
модуляции М в выражении АМ тонального радиосигнала, а спектр радиосигнала с
угловой модуляцией имеет вид, показанный на рис. 12.
. Индекс угловой
модуляции m играет такую же роль, как коэффициент амплитудной
модуляции М в выражении АМ тонального радиосигнала, а спектр радиосигнала с
угловой модуляцией имеет вид, показанный на рис. 12.
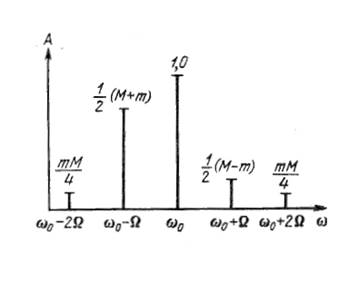
Рис. 12
Однако можно обнаружить и существенное различие
спектров АМ радиосигнала и радиосигнала с угловой модуляцией: в спектре радиосигнала
с угловой модуляцией составляющая нижней боковой частоты имеет дополнительный
фазовый сдвиг равный ![]() .
.
При этом и векторные диаграммы АМ и ФМ (ЧМ)
радиосигналов существенно отличаются: в векторной диаграмме радиосигнала с
угловой модуляцией модуляционный вектор перпендикулярен к вектору несущей (рис.
12). Незначительное изменение длины суммарного вектора ![]() от вектора несущей
от вектора несущей ![]() обусловлен приближённым характером анализа, и
при очень малых значениях m ими можно пренебречь.
обусловлен приближённым характером анализа, и
при очень малых значениях m ими можно пренебречь.
Сравнение однотональных ЧМ и ФМ радиосигналов. Выражения ЧМ и ФМ радиосигналов, если
положить ![]() совпадают с точностью
постоянной фазы
совпадают с точностью
постоянной фазы ![]() . Векторные
диаграммы ЧМ и ФМ радиосигналов совпадают.
. Векторные
диаграммы ЧМ и ФМ радиосигналов совпадают.
Однако между ними имеется и различие: зависимости
параметров ЧМ и ФМ радиосигналов различны при изменении амплитуды и частоты модулирующего
сигнала. При ФМ ![]() и
и ![]() , а при ЧМ
, а при ЧМ
![]() и
и 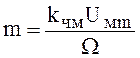 . Зависимости параметров ФМ и ЧМ радиосигналов
от частоты модулирующего сигнала приведены на рис. .
. Зависимости параметров ФМ и ЧМ радиосигналов
от частоты модулирующего сигнала приведены на рис. .
Рис.
Спектральное разложение ЧМ и ФМ радиосигналов при любых значениях индексах модуляции. Для простейшего случая однотонального ЧМ (ФМ) радиосигнала можно найти общее выражение спектра, справедливое при любых значениях индекса фазовой модуляции m.
Выражение радиосигнала с угловой модуляцией запишем в следующем виде:
![]()
![]() .
()
.
()
В курсе высшей математики, посвящённым специальным
функциям, доказывается, что экспонента ![]() с мнимым
показателем, периодическая на отрезке
с мнимым
показателем, периодическая на отрезке ![]() , разлагается в комплексный ряд Фурье
, разлагается в комплексный ряд Фурье
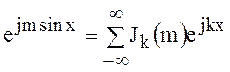 ,
()
,
()
где m – любое вещественное число; ![]() - функция Бесселя
первого рода k-го индекса от аргумента m
- функция Бесселя
первого рода k-го индекса от аргумента m ![]() .
.
Полагая в формуле () ![]() имеем
имеем 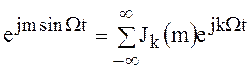 , тогда для выражения радиосигнала с угловой модуляцией получим
, тогда для выражения радиосигнала с угловой модуляцией получим
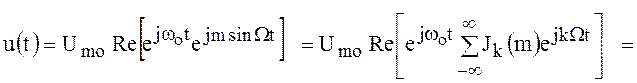
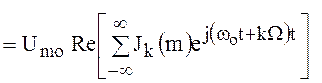 .
.
Отсюда, учитывая () получаем следующее выражение ЧМ (ФМ) радиосигнала с любым значением индекса модуляции m:
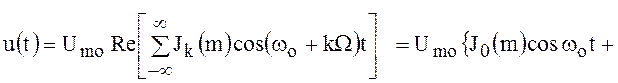
![]()
![]() . ()
. ()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.