Характеристики детерминированных сигналов. Представление произвольного сигнала в виде суммы элементарных колебаний, страница 25

Из сравнения выражений () и () следует, что при  < 1форма АЧХ усилителя с ПОС такая же, как и усилителя без обратной связи. Однако, в усилителе с ПОС резонансный коэффициент усиления увеличивается в 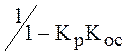 раз; во столько же раз возрастает эквивалентная добротность колебательного контура усилителя и соответственно уменьшается его полоса пропускания.

a                                                                b

Рис.

Эти явления обусловлены с тем, что в усилителе с ПОС происходит регенерация, т.е. частичная компенсация потерь в колебательном контуре за счёт энергии преобразования источника питания.

Для осуществления ПОС в резонансном усилителе можно использовать катушку индуктивности, включённую последовательно во входную цепь, и индуктивно связанную с колебательным контуром. Несмотря на простоту, резонансные усилители с ПОС находят применение редко из-за их склонности к самовозбуждению при   1.

3.7. Устойчивость активных линейных цепей с обратной связью

В настоящем параграфе рассматриваются основы теории устойчивости состояния равновесия АЛЦ с обратной связью.

Рассмотрим усилитель с передаточной функцией , выход которого соединён со входом четырёхполюсника обратной связи с передаточной функцией . Полагаем, что внешний входной сигнал отсутствует.

Рис. 3.

Изображение выходного сигнала , откуда

.                                                                 (3.  )

Поскольку в системе возникли колебания с амплитудой , то равенство () справедливо только при тех значениях р, которые являются корнями характеристического уравнения

.                                                                               (3. )

Пусть , , - корни характеристического уравнения.

Так как рассматриваемая система линейна, то в общем случае выходное напряжение запишется в следующем виде:

                                                           (3. )

Это напряжение не будет нарастать во времени, если все корни характеристического уравнения имеют отрицательные вещественные части, т.е. располагаются в левой полуплоскости комплексной переменной р. Поэтому, АЛЦ будет устойчивой, если корни характеристического уравнения расположены в левой полуплоскости комплексной переменной р.

a                                                         b

Рис.

При синтезе и анализе АЛЦ с обратной связью возникают две задачи. Если синтезируемая цепь, например усилитель, должна быть устойчивой, требуется критерий устойчивости, который позволил бы по виду функций  и  судить об отсутствии корней характеристического уравнения в правой полуплоскости. Если, наоборот, обратная связь используется для создания автогенератора, то корни характеристического уравнения должны располагаться в правой полуплоскости комплексной переменной р.

Алгебраический критерий устойчивости(критерий Рауса - Гурвица) . Предположим, что усилитель, так и четырёхполюсник обратной связи являются линейными цепями с сосредоточенными параметрами и, следовательно, передаточные функции

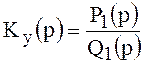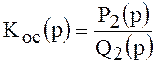 и                                                           (3. )

являются отношениями многочленов по степеням р. Подставив формулы () в () ,получим характеристическое уравнение системы:

.                                                                 (3. )

Отсюда следует, что система с обратной связью устойчива, если все корни характеристического уравнения

имеют отрицательные вещественные части. В алгебре многочлены  с такими свойствами называют многочленами Гурвица.

Приведём окончательную формулировку критерия устойчивости Гурвица. Для того, чтобы действительные части всех корней характеристического уравнения

с действительными коэффициентами и  были отрицательными, необходимо и достаточно, чтобы были положительными все определители , ,              , составленные из коэффициентов , , ,  

 последующей схеме:

, , ,

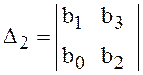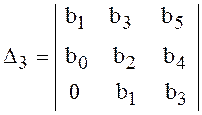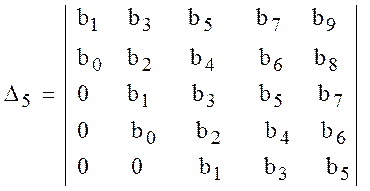 и т.д.

Сформулированный алгебраический критерий устойчивости называется критерием Рауса-Гурвица.