Характеристики детерминированных сигналов. Представление произвольного сигнала в виде суммы элементарных колебаний, страница 10

С уменьшением отношения  (за счёт ) лепестки спектра убывают медленнее и в пределе при стремлении отношения 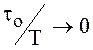, спектр приобретает (см. рис. 20 б) строго периодическую структуру, а уровень лепестков стремится к нулю.

20 б

Если одновременно с уменьшением  увеличивать Е так, чтобы произведение , площадь тактового импульса оставалась неизменной и равной, например, единице , то при  выражение (98) переходит в формулу

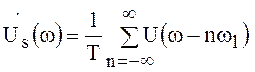.                                                                     (99)

Таким образом, совершён переход от тактовых импульсов прямоугольной формы с конечной амплитудой к тактовым импульсам, характеризуемым дельта-функциями, так что можно записать

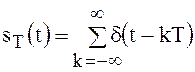.                                                                             (100)

Соответственно выражение дискретизованного сигнала запишется в виде

.                  (101)

График спектра для этого случая приведен на рис. 21.

Рис. 21

Представление  в форме (102) существенно упрощает его спектральный анализ. Применив к выражению (102) прямое преобразование Фурье, получим

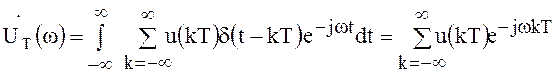.               (103)

Полагая, что дискретизация аналогового сигнала начинается с момента времени , перепишем последнее выражение в виде

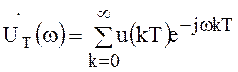.                                                                     (104)

По своей размерности функции  и  неодинаковы:

Первая имеет размерность [В/Гц], а вторая – просто [В] (если  и  - напряжения). Преимуществом выражения (104) является возможность определения спектра  по совокупности временных отсчётов , без обращения к спектру  исходного аналогового сигнала и независимо от соотношения между Т и .

1.9. Интеграл Дюамеля

Рассмотрим прохождение сигнала через фильтр с известной передаточной функцией. Пусть сигнал на входе фильтра  имеет спектр , тогда сигнал на выходе  имеет спектр , где  - передаточная функция фильтра.

Используя обратное преобразование Фурье, найдём по выходному спектру выходной сигнал. Если на входе фильтра действует единичный импульс напряжения  со спектральной плотностью , то спектр выходного напряжения равна передаточной функции . Следовательно, отклик на единичный импульс, т.е. импульсная характеристика (функция) фильтра, определяется с помощью ОПФ, применённого к передаточной функции :

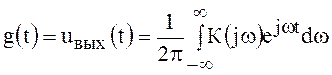.                                                      (105)

Произведению двух спектров  соответствует функция времени , являющаяся свёрткой функций  и :

.                                                  (106)

Если входной сигнал равен нулю до момента , то напряжение на выходе физически реализуемого фильтра не может возникнуть раньше этого времени. Поэтому нижний предел интегрирования в (106) можно заменить нулём:

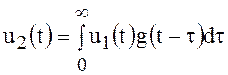.                                                                       (107)

Это выражение называется интегралом Дюамеля, записанным в импульсной форме. Физически это означает, что входное напряжение представляется в виде суммы дельта-функции, соответствующих разным моментам времени, с амплитудами, равными мгновенным значениям сигнала в эти моменты 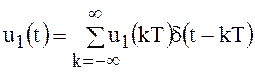, а выходное напряжение равно сумме откликов фильтра на эти дельта-функции.

Выражения (106) и (107) имеют важное значение, поскольку позволяют находить выходное напряжение фильтра  по заданным  и .

1.11. Сигналы на выходе идеального фильтра нижних частот

Пусть имеется идеальный фильтр нижних частот с передаточной функцией

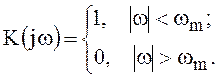
Здесь  - граничная круговая частота ФНЧ.

Импульсная функция ФНЧ равна

.                                                                (108)

Такой ФНЧ физически нереализуем, так как импульсная функция не равна нулю в области отрицательных значений времени. Несмотря на физическую реализуемость, такая модель ФНЧ часто используют для приближённого описания частотных фильтров, полагая, что передаточная функция  содержит фазовый множитель, линейно зависящий от частоты (рис. 22):

Несложно проверить, что такому ФНЧ соответствует импульсная функция

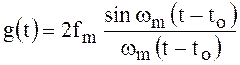.                                                                  (109)