Это выражение, называемое неравенством Бесселя, справедливо для любой системы базисных функций.
Ортогональная система функций называется полной, если при увеличении числа слагаемых ряда среднеквадратичную ошибку можно сделать сколь угодно малой.
Условие полноты можно представить в виде соотношения
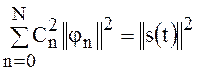 .
(9)
.
(9)
При выполнении этого условия можно полагать, что ряд (5) сходится в среднем, т.е.
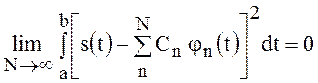 .
(10)
.
(10)
Из этого, ещё не следует, что ряд  сходится к функции
сходится к функции ![]() , т.е. что
, т.е. что
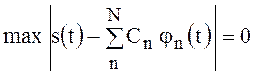
при любых значениях t. При некоторых значениях t ряд 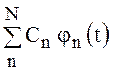 может отличаться от функции
может отличаться от функции
![]() , хотя равенство (10)
имеет место.
, хотя равенство (10)
имеет место.
Для системы комплексных базисных функций ![]() приведенные выше
определения записываются следующим образом:
приведенные выше
определения записываются следующим образом:
условие ортонормированноcти
 ; (11)
; (11)
квадрат нормы базисных функции
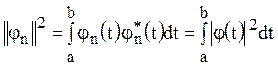 ;
(12)
;
(12)
коэффициенты обобщённого ряда Фурье
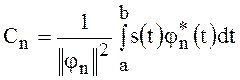
![]() .
(13)
.
(13)
В этих выражениях функция ![]() - функция
комплексно-сопряжённая с функцией
- функция
комплексно-сопряжённая с функцией ![]() .
.
Если ![]() -
напряжение или ток, то
-
напряжение или ток, то ![]() есть
мгновенная мощность, выделяемая на сопротивлении в 1 Ом, а квадрат нормы
функции
есть
мгновенная мощность, выделяемая на сопротивлении в 1 Ом, а квадрат нормы
функции ![]() будет определять
энергию сигнала
будет определять
энергию сигнала
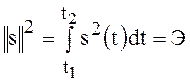 .
(14)
.
(14)
В формулу (14), подставляя выражение сигнала 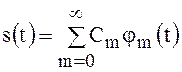 , получим
, получим
 .
.
В соответствии с выражением (14) энергия сигнала
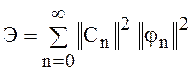 .
(15)
.
(15)
При использовании ортонормированной системы базисных функций
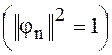 выражение энергии сигнала соответственно равно
выражение энергии сигнала соответственно равно
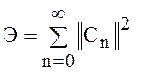 .
(16)
.
(16)
При этом имеется в виду, что интервал времени, ![]() в котором определяется
энергия Э, является интервалом ортогональности для системы базисных функций
в котором определяется
энергия Э, является интервалом ортогональности для системы базисных функций ![]() .
.
Отношение
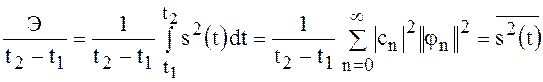 (17)
(17)
определяет среднюю за интервал времени ![]() мощность сигнала.
мощность сигнала.
Выбор системы предопределяется видом сигналов, задачами и методом анализа (или синтеза).
1.2. Гармонический анализ периодических сигналов. Ряд Фурье
При разложении периодического сигнала ![]() с периодом Т в ряд Фурье
в качестве ортогональной системы используют систему гармонических колебаний
кратных частот
с периодом Т в ряд Фурье
в качестве ортогональной системы используют систему гармонических колебаний
кратных частот
1, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…
,… ![]() ,
, ![]() ,… (18)
,… (18)
или систему комплексных колебаний
![]() ,
,
![]() ,
, ![]() , 1,
, 1, ![]() ,
, ![]() ,…
,…![]() ,… (19)
,… (19)
Интервал ортогональности в обеих систем базисных
функции совпадает с периодом  сигнала
сигнала
![]() .
.
В качестве периодического сигнала, рассмотрим
напряжение, заданное на интервале значений времени ![]() < t <
< t < ![]() и удовлетворяющее
условиям
и удовлетворяющее
условиям ![]() , состоящее из суммы
гармонических составляющих, являющихся рядом Фурье:
, состоящее из суммы
гармонических составляющих, являющихся рядом Фурье:
 .
(20)
.
(20)
Совокупность коэффициентов ![]() ряда Фурье в базисе
тригонометрических функций называется частотным спектром периодического сигнала.
Коэффициенты ряда (20)
ряда Фурье в базисе
тригонометрических функций называется частотным спектром периодического сигнала.
Коэффициенты ряда (20) ![]() определяются
с помощью формул, приведенных в предыдущем параграфе.
определяются
с помощью формул, приведенных в предыдущем параграфе.
Из выражения (13) следует, что
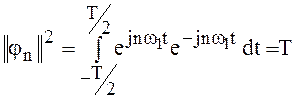 .
(21)
.
(21)
Применяя формулу (21), находим
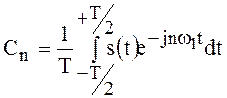 .
(22)
.
(22)
Коэффициент ![]() является
комплексной величиной, определяющей амплитуду и фазу n-ой
гармоники основной частоты
является
комплексной величиной, определяющей амплитуду и фазу n-ой
гармоники основной частоты 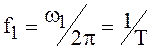 .
.
Поскольку ![]() ,
то
,
то
 ,
(23)
,
(23)
где действительная и мнимая части коэффициента ![]() определяются формулами
определяются формулами
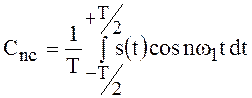 ,
(24)
,
(24)
 .
(25)
.
(25)
Коэффициенты ![]() часто бывает удобно
представлять в показательной форме
часто бывает удобно
представлять в показательной форме
![]() ,
(26)
,
(26)
где ![]() ,
(27)
,
(27)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.