Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 9

1)  определение статической характеристики случайных входных и выходных сигналов;

2)  с использованием данных статических характеристик определяются динамические свойства (передаточная функция, АФХ, и т.д.).

2.6.1.  Свойства и характеристики стационарных случайных процессов

Случайные процессы статические характеристики, которых не изменяются во времени называются стационарными. Эти характеристики определяются путем осреднения ординат данного случайного процесса или по времени, или по множеству реализаций данного случайного процесса. Если результаты осреднения одинаковы, то данный случайный процесс называется эргодическим.

Основными характеристиками случайных стационарных эргодических процессов является:

1)   Математическое ожидание:

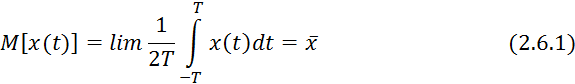
где  — время реализации случайного процесса.

Основные статистические характеристики удобно определить с использованием центрированных значений случайного процесса:

2)   Для расчета линейных систем информация содержится в их корреляционных функциях:

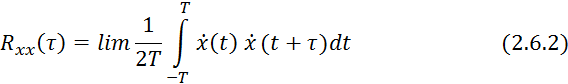
где  — время сдвига между ординатами случайного процесса.

Данная функция показывает насколько ордината случайного процесса () связана с ординатой случайного процесса через время сдвига .

Свойства корреляционной функции:

а)   она имеет четный характер: ;

б) 

в)   

г)   

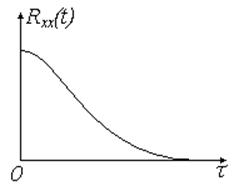
Рис. 11

3)   Если изучается взаимосвязь между  и , то применяется взаимокорреляционная функция:  

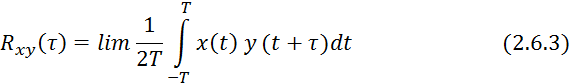
Свойства корреляционной функции:

а)   данная функция имеет не четный характер;

б)   

4)   При частном анализе СУ используют статические частотные характеристики:

4.1)  Спектральная плотность:                          

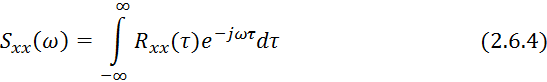
Физический смысл спектральной плотности характеризует часть (долю) мощности случайного процесса для определенного интервала частот.

4.2)  Взаимоспектральная плотность:    

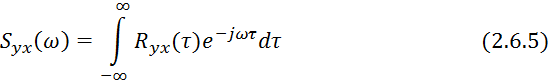
Обратное преобразование Фурье:

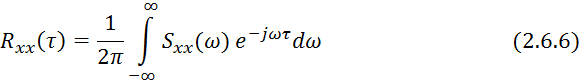
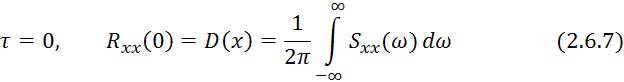
5)   При прохождении случайного сигнала  через некоторую линейную систему  его характеристика изменяется  — сигнал на выходе.

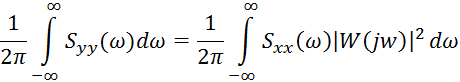
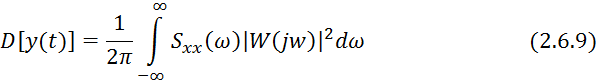
6)   Взаимоспектральная плотность и спектральная плотность связаны следующим соотношением:

7)   Взаимосвязь между взаимокорреляционной функцией и импульсной функциями определяется:

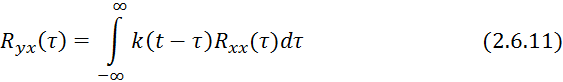
Зависимости 2.6.8÷2.6.11 используются для определения динамических характеристик объектов при действии на эти объекты стационарных случайных процессов.

2.6.2  Постановка эксперимента по определению статистических характеристик процессов

Определение корреляционных функций может быть произведено при конечном времени .

Формулы:

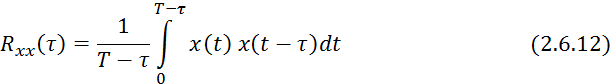
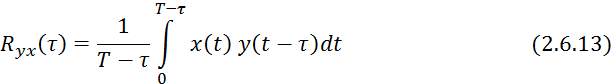
 и , рассчитанные по формулам 2.6.12 и 2.6.13, являются оценками истинной функции. 

Если математическое ожидание оценки приблизительно равно истинному значению, то такие оценки являются несмещенными, однако их отклонение бывает значительным, особенно при больших значениях 𝜏.

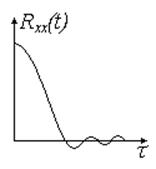
Рис. 12

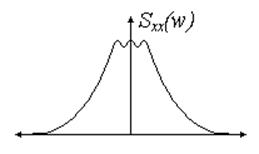
Рис. 13

При применении ЭВМ для расчета корреляционных функций необходимо получить ряд дискретных значений ординат  и  равноотстающих друг от друга на интервал времени .

 выбирается таким образом, чтобы зависимость на данном интервале между двумя ординатами была линейной:

а)   формула для расчета числа ординат случайного процесса:

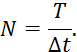
б)   формула для расчета количества ординат соответствующих сдвигу:

С учетом данных преобразований формулы 2.6.12 и 2.6.13 примут вид:

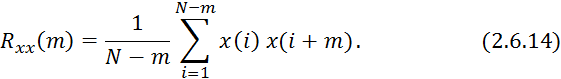
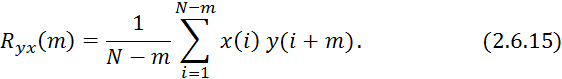
Расчет по формулам 2.6.14 и 2.6.15 зависит от следующих факторов:

1)  от точности реализации случайного процесса;

2)  от величины :

а)  , где  — частота максимальной гармоники случайного процесса; б) на практики применяют следующую формулу , где  — средняя скорость изменения случайного процесса: , где  — количество пересечений случайным процессом линии соответствующей средней ординате случайного процесса. Как правило, ,  — время за которое случайный процесс пересечет 100 раз среднее значение случайного процесса;

3)  𝜏 — величина временного сдвига. С увеличением 𝜏 точность корреляционной функции уменьшается ;