Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 18

3.5.  Диффузионные модели

Согласно теории массообмена диффузия бывает молекулярная и конвективная. Молекулярная — процесс проходит на микроуровне, конвективная — перенос вещества осуществляется его частицами, то есть процесс проходит на макроуровне.

·  Однопараметрическая диффузионная модель. Перемешивание частиц в продольном направлении характеризуется коэффициентом ,

·  Двухпараметрическая диффузионная модель. Данный поток характеризуется коэффициентом продольного перемешивания  и коэффициентом радиального перемешивания .

3.5.1.  Однопараметрическая диффузионная модель (ОДМ)

Допущение: за структуру потока принимаем следующее:

Технологическая среда перемешивается в канале со средней линейной скоростью , при этом происходит перемешивание частиц в продольном направлении за счет обратного потока при равномерном распределении концентрации вещества в сечениях перпендикулярных направлению движения потока.

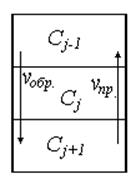
Рис. 23

, , ,

 

;

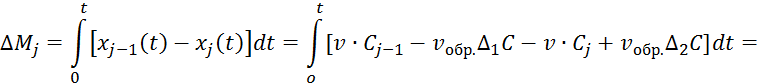
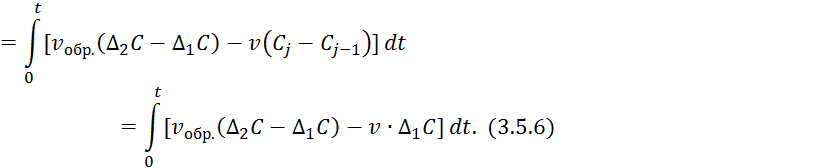
Разделим выражение 3.5.6 на :

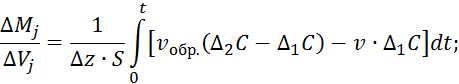
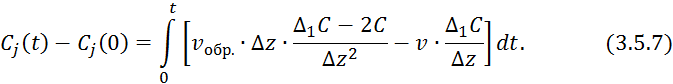
Продифференцируем по времени обе части выражения 3.5.7:

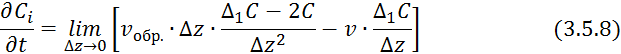
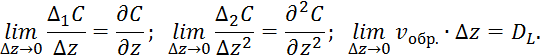
 — коэффициент продольного перемещения.

Коэффициент  определяется расчетным экспериментальным путем. При экспериментальном определении используется критерий Пекле:

Трудность решения уравнения 3.5.9 связана с нахождением граничных условий и нахождением .

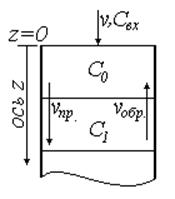
Рис. 24

Для нестационарного режима ячейки:

При предельных значениях , накопление вещества не происходит:

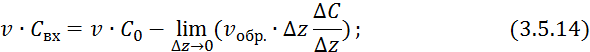
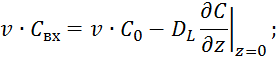
Получим второе граничное условие при :

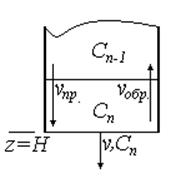
Рис. 24

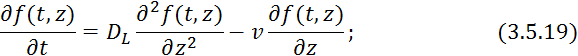
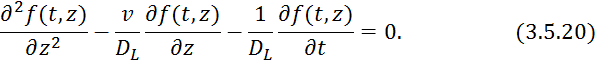
Преобразуем по Лапласу по времени 3.5.20:

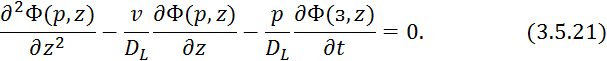
Решением 3.5.21 является:

где

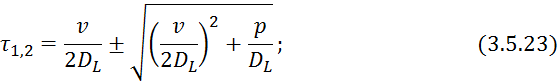
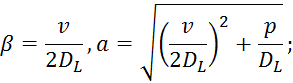
Преобразуем по Лапласу по времени граничные условия 3.5.15 и 3.5.18:

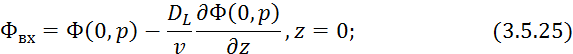
Продифференцируем выражение 3.5.24 по z:

В выражение 3.5.25 подставляем 3.5.28 и 3.5.29:

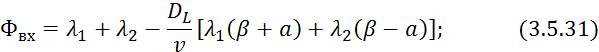
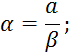
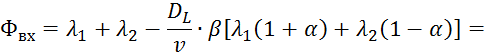
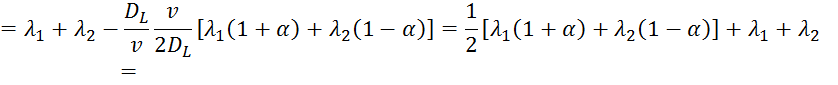
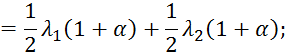
3.5.26 подставим в 3.5.30:

Имеем систему из двух уравнений 3.5.32 и 3.5.34 с двумя неизвестными  и . Решение данной системы имеет следующий вид:

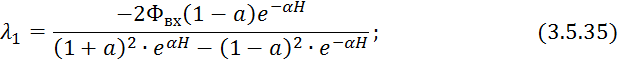
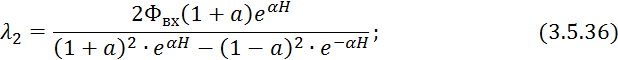
Представляем величины  и  в 3.5.34:

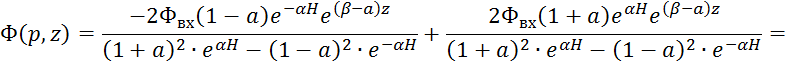
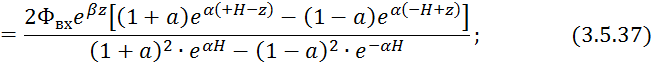
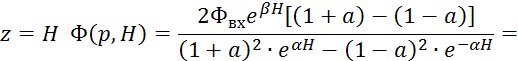
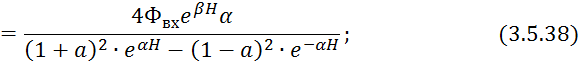
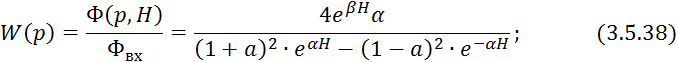
Не решая 3.5.40 приведем графики расчетных  и  кривых.

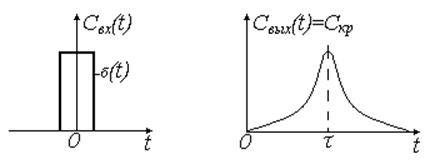
Рис. 25

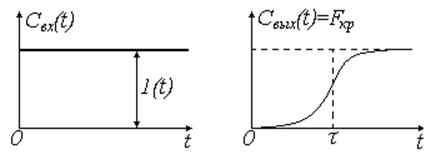
Рис. 26

При моделировании неизвестной структурой потока, если экспериментальные  и  кривые совпадают с расчетными, то неизвестную модель можно описать ОДМ. Данная модель лучше описывает динамику аппаратов работающих по принципу вытеснения. Данная модель хорошо описывает гидродинамику колонных аппаратов.

3.5.2.  Двухпараметрическая диффузионная модель

За структуру принимается следующее:

Некоторая технологическая среда перемещается в продольном радиальном канале длиной  и радиусом  со скоростью , при этом происходит перемешивание частиц среды, как в продольном, так и в радиальном направлении.

Уравнение двухпараметрической диффузионной модели (ДДМ):

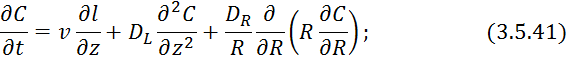
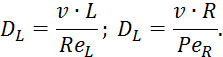
Данная модель сложна и применяется только в научных исследований.

3.6.  Ячеечная модель

При выводе уравнения данной модели принимаются допущения:

1)  Реальный поток состоит из  последовательно соединенных ячеек;

2)  В каждой ячейке осуществляется режим идеального перемешивания;

3)  Перемешивание между ячейками отсутствует;

4)  скорость всех частиц одинакова;

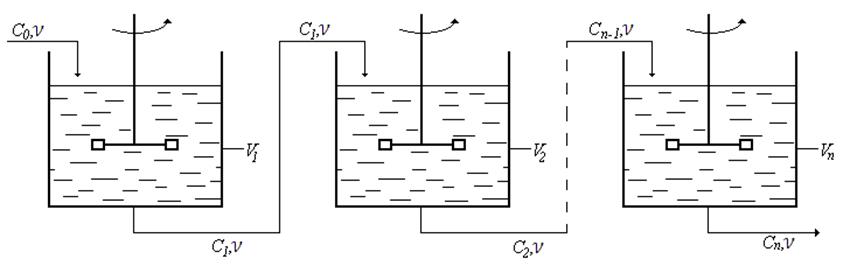
 Рис. 27

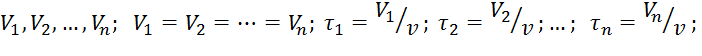
Для каждой -той ячейки можно записать:

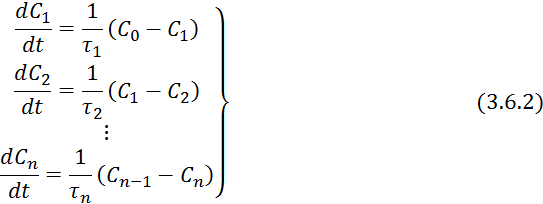
Рис. 28

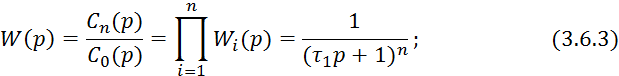
Если объемы не равны, то

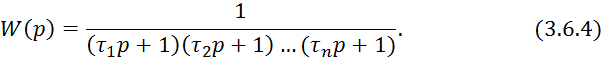
Для колонного аппарата:

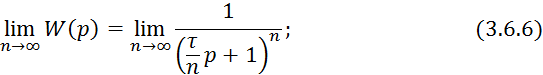
Обозначим

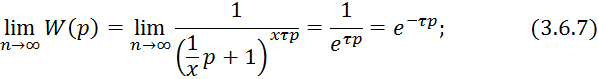
Решим систему 3.6.2. при импульсном входном воздействии, то есть при

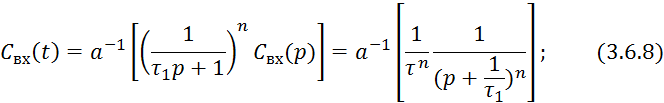
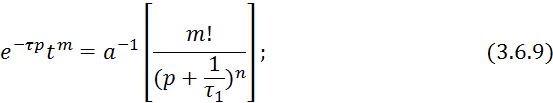
3.6.9 берется из таблицы преобразований Лапласа.

Пусть , ;  

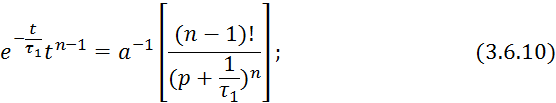
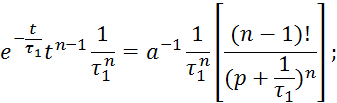
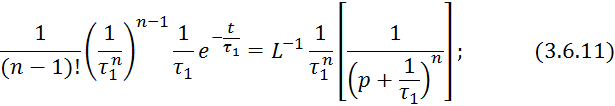
Правые части 3.6.8. и  3.6.11 равны, поэтому равны и левые части этих выражений.

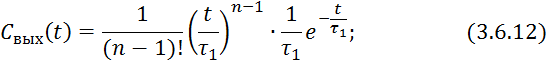
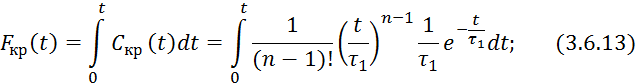
Проведя интегрирование, получим частям выражения 3.6.13 получим:

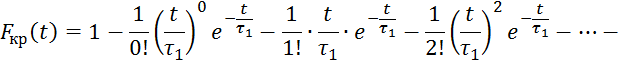
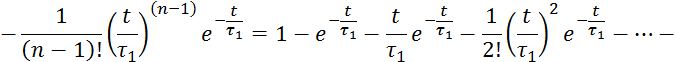
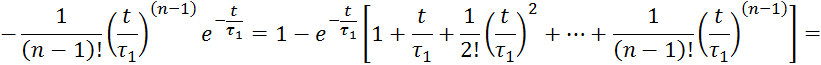
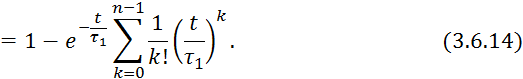
Выражение 3.6.12 и 3.6.14 является  и  кривыми. Для колонного аппарата:

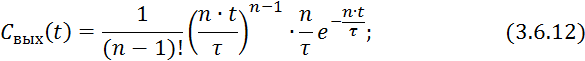
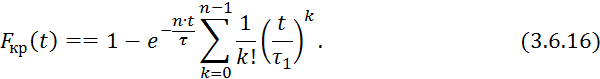
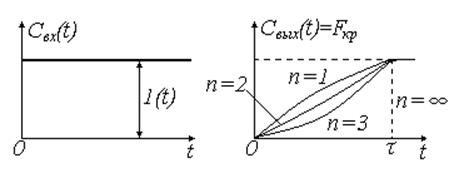
Рис. 29

где  — число ячеек.

В химической технологии широко применяются аппараты секционирования по высоте сетчатыми перегородками. Для математического описания таких аппаратов ячеечная модель малопригодна и применяется ячеечная модель с обратным потоком [3].

4.  Математическое описание тепловых процессов

Тепловые процессы протекают в теплообменных аппаратах. При выводе математических моделей этих аппаратов принимаются следующие допущения: