Математическая модель без учета тепловой инерции стенки будет иметь следующий вид:
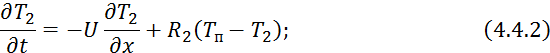
где
— температура хладагента, а
.
Математическая модель с учетом накопления тепла в стенке:
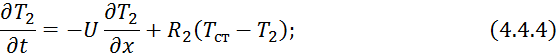
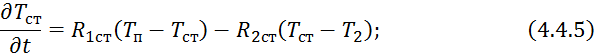
4.5. Передаточные функции теплообменных аппаратов
4.5.1 Конденсатор без учета накопления тепла в станке
Математическая модель имеет следующий вид:
где
— температура хладагента;
— температура пара.
Начальные условия для уравнения 4.5.1:
Граничные условия:
Структурная схема:
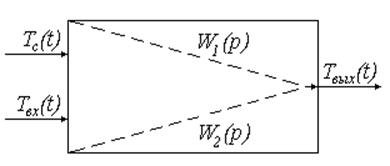
Рис. 33
Второе граничное условие:
Преобразуем по Лапласу по времени при начальных условиях 4.5.2 уравнение 4.5.1:
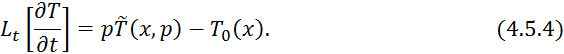
, где 
символ преобразования по времени.
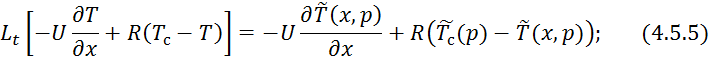
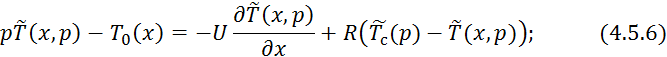
4.5.7 является граничным условием для 4.5.6.
Преобразуем по Лапласу по линейной координате уравнение 4.5.6 с учетом граничных условий 4.5.7:
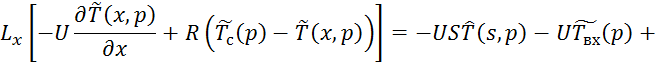
Прировняем 4.5.9 и 4.5.10:
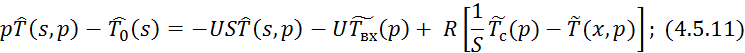
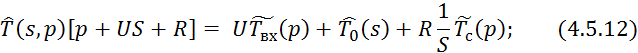
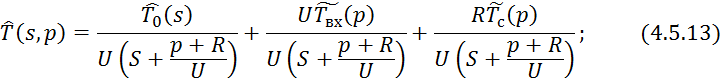
Применим обратное преобразование по Лапласу по линейной координате выражение 4.5.13:
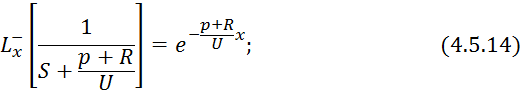
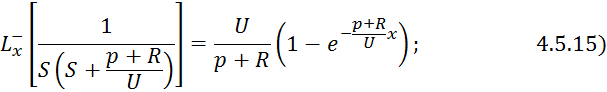
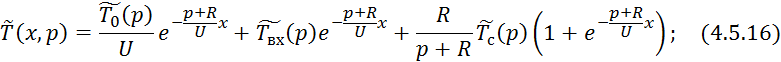
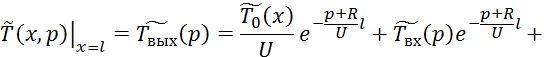
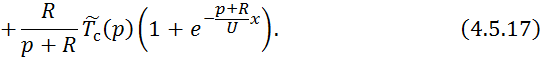
При
значительной длительности режима 
:
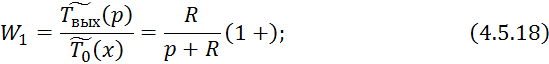
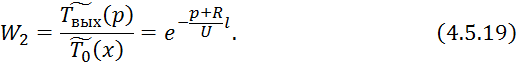
4.5.2 Конденсатор с учётом накопления тепла в стенке
Математическая модель данного теплообменника имеет вид:
, 
, 
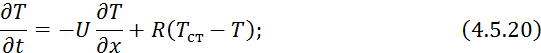
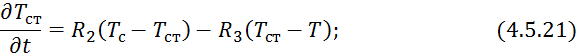
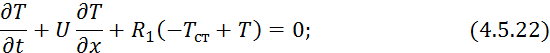
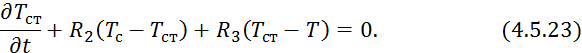
Начальные и граничные условия:
Преобразуем по Лапласу по времени 4.5.22 4.5.23:
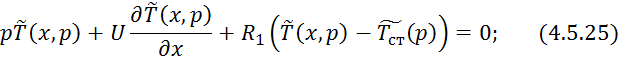
Преобразуем уравнение 4.5.25:
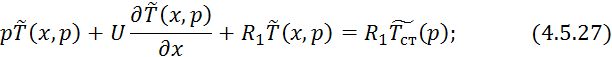
Преобразуем уравнение 4.5.26:
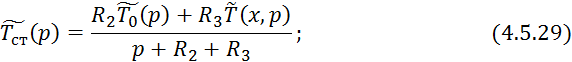
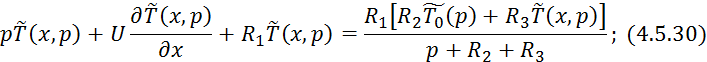
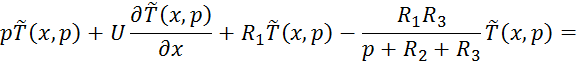
Уравнение 4.5.32 является граничным условием для 4.5.31.
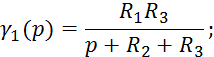
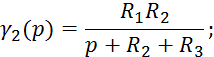
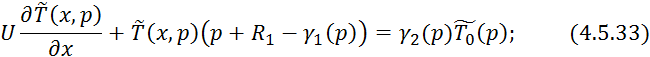
Преобразуем по Лапласу по линейной координате 4.5.33 при 4.5.32:
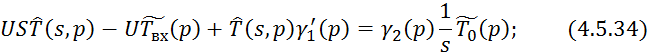
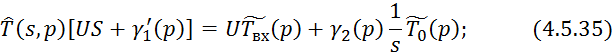
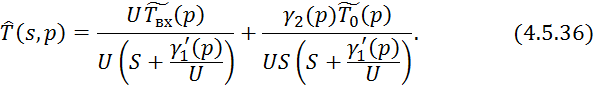
Произведем обратное преобразование по Лапласу по линейной координате уравнения 4.5.36:
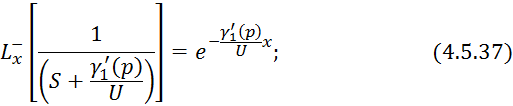
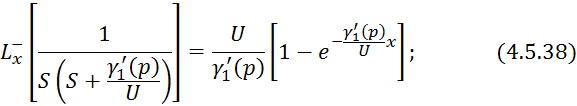
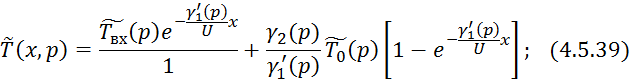
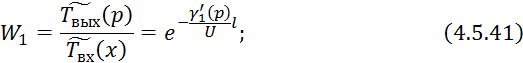
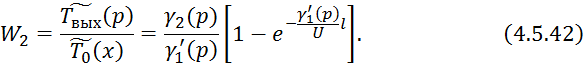
4.5.3 Кожухотрубчатый противоточный теплообменник
Математическая модель:
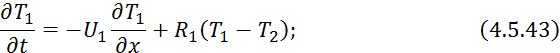
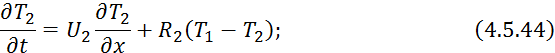
Преобразуем по Лапласу по времени при нулевых начальных условиях 4.5.43 и 4.5.44:
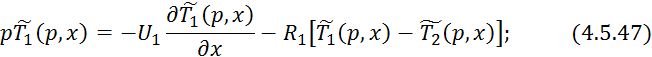
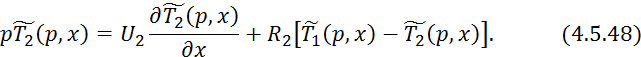
Преобразуем 4.5.47:
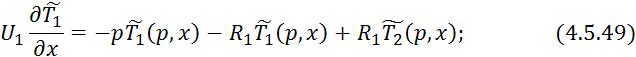
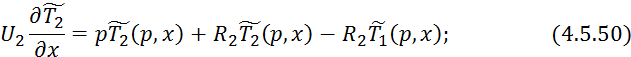
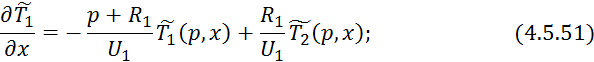
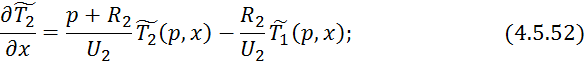
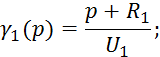
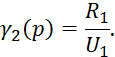
Для решения данной системы уравнений составим матрицу:
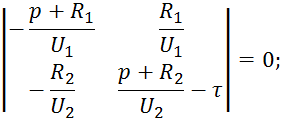
где
— корни матрицы.
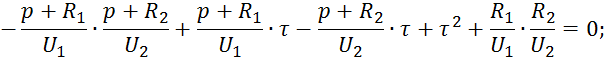
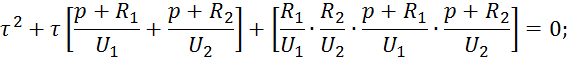
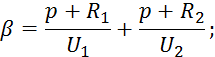
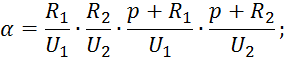
Решение уравнений 4.5.51 и 4.5.52 с учетом 4.5.54 примет следующий вид:
где 
, 
, 
, 
— постоянные интегрирования, которые находятся из
граничных условий.
Продифференцируем
по 
уравнение 4.5.55:
: 
: 
Получим
граничное условие для 
из уравнения 4.5.55:
Из 4.5.63 определим :
Подставляем 4.5.65 в 4.5.61:
Из
выражения 4.5.64 найдем :
Подставляя 4.5.67 в 4.5.66:
Умножаем
левую и правую часть 4.5.68 на 
:
Выражение
4.5.62 домножим на 
:
Так как левые части уравнений 4.5.69 и 4.5.70 равны, то равны их правые части:
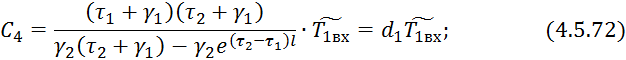
Подставляем 4.5.72 в 4.5.67:
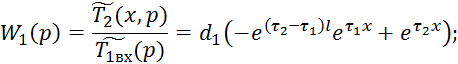
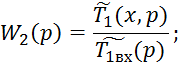
Для нахождения и необходимо использовать выражение 4.5.61 и 4.5.62.
Примечание: уравнения 4.5.51 и 4.5.52 нельзя преобразовывать по Лапласу по линейной координате, то есть они имеют различные граничные условия.
5. Математическое моделирование массообменных аппаратов
5.1. Математическая модель процесса газоабсорбции
Схема газового абсорбера колонного типа со слоем осадка имеет следующий вид:
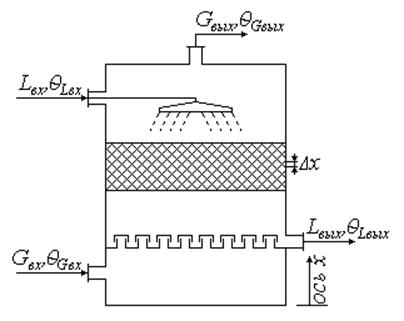
Рис. 33
где
, 
— весовые расходы абсорбента (жидкость);
, 
— весовой расход газовой смеси;
, 
— концентрация поглощаемого компонента в жидкой
фазе;
, 
— концентрация поглощаемого компонента в газе.
Уравнение массообмена:
где
— удельный поток поглощаемого компонента из газа в
жидкость;
— коэффициент массопередачи.
— равновесная концентрация поглощаемого компонента
в газовой смеси;
, 
.
Выделим
участок в слое осадка длинной 
.
Принимаем равномерное распределение газа и жидкости по всему слою осадка.
Для вывода математической модели используются следующие уравнения:
где 
— количество вещества накапливаемого в данном слое;
— количество вещества поступающего в слой:
— количество вещества уходящего из слоя.
В процессе массообмена происходит изменение объемов жидкой и газовой фаз в данном слое.
где 
— удельный объем жидкой фазы;
— удельный объем газовой фазы;
— удельный объем насадки.
где
— площадь сечения адсорбера;
— плотность жидкости.
Подставим 5.1.5 и 5.1.6 в 5.1.2, получим:
Уравнение 5.1.8 называется уравнением неразрывности жидкости.
Чтобы
полностью определить выражение 5.1.8 необходимо определить взаимосвязь между 
и :
где
— толщина слоя жидкости;
— поверхность насадок.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.