Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей

Курс лекций по дисциплине

«Моделирование объектов и систем управления отрасли»

для студентов специальности « Автоматизация технологических процессов»

Автор- доц. Кафедры АППиЭ Кобринец В.П.

Введение

Основная задача моделирования объектов и систем управления — повышение эффективности химико-технологического процесса. Решение этой задачи возможно только с применением методов кибернетики (). На основании данных моделей можно синтезировать системы управления и сократить сроки освоения технологий. Математическая модель конкретного процесса которая отражает основные взаимосвязи между параметрами химико-технологического процесса, позволяет в процессе экспериментов и реализации расчетов на химико-технологическом процессе сократить сроки освоения химико-технологического процесса, и следовательно ускорить технологический процесс.  

1.  Методы моделирования объектов и систем управления

Моделирование заключается в том, что исследование объектов и систем проводится на их моделях, а результаты должны быть перенесены на химико-технологический процесс. К процессу моделирования предъявляют следующие требования:

1)  эксперимент на модели должен быть проще, экономичнее, безопаснее;

2)  должно существовать правило переноса свойств модели на оригинал.

Моделирование базируется на подобии объектов: один объект — оригинал, второй — его модель.

Подобные — объекты, у которых технологические параметры отличаются в определенное число раз (масштаб подобия).

Два метода моделирования: физическое и математическое.

Физическое  моделирование основано на физическом подобии модели и оригинала. В этом методе должны быть подобны физические свойства модели и оригинала.

Математическое основано на математическом подобии модели и оригинала, то есть модель и оригинал могут иметь различную природу но их математическое описание должно быть идентичным.

Математическое подобие может быть: символьным (знаковым) и реальным (вещественным).

Изучение свойств объекта посредством изучения свойств его модели называется моделированием. На практике различают следующие процессы моделирования:

1)  моделирование по принципу геометрического подобия и модели и оригинала — геометрическое подобие;

2)  физическое моделирование — здесь кроме геометрического подобия присутствует физического подобия;

3)  математическое моделирование.

Достоинства методов физического моделирования:

а)  физическая модель воспроизводит все физические свойства оригинала;

б)  измерение технологических параметров физической модели можно производить теми же средствами, что и в оригинале — это уменьшает погрешность измерений;

в)  данная модель может применяться для моделирования объектов для которых невозможно создание математических моделей.

Недостатки методов физического моделирования:

а)  большая трудоемкость в создании моделей сложных АТП;

б)  изменение параметров оригинала требует дорогостоящей реконструкции его модели;

в)  невозможность создания физических моделей некоторых АТП, в частности, для химических реакторов.

Достоинства математического моделирования: а)  простота создания моделей;

б)  изменение параметров оригинала не требует сложных изменений у модели.

Недостатки математического моделирования:

а)  невозможность создания математических моделей для некоторых процессов.

1.1.  Физическое моделирование объектов и систем управления

Математической основой физического подобия является теория подобия и др. При разработке физической модели применяются методы  подобия и аналогии.

1.1.1.  Метод подобия

Подобие — перенос данных исследования модели на оригинал. Это свойство называется свойством традуктивности. Согласно теории подобия — критерии подобия в сходных точках модели и оригинала должны быть равны. Они устанавливают сходство модели и оригинала, и являются полной мерой переноса данных модели на оригинал.

А)  Условие подобия по одному критерию.

Пример: необходимо смоделировать распределение скоростей жидкости в канале сложной фоормы.

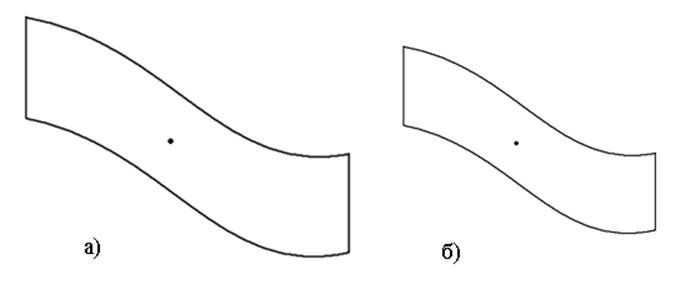
Рис.1 Изображение оригинала а) и модели б)

Критерий подобия — гидродинамический критерий Рейнольдса:

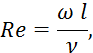
где  — скорость движения среды в канале;

 — длина участка;

 — динамический коэффициент вязкости.

  

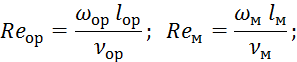
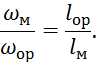
Б)  Условие подобия по двум критериям.

Пример 1.: необходимо построить физическую модель химического реактора.

Процессы в химическом реакторе характеризуются:

1)  критерий подобия химического превращения (критерий Данклера):

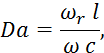
где   — скорость превращения;

 — скорость потока;

 —концентрация.

2)  гидродинамический критерий Рейнольдса:

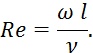
 (при уменьшении длины  для соблюдения подобия химического превращения необходимо уменьшать скорость ).

 (при уменьшении длины  необходимо увеличивать скорость ).

В модели реактора оба эти критерия несовместимы.

Возможность применения физического моделирования определяется следующим соотношением:

.

где   — число параметров модели;

 — число параметров оригинала;

 — число критериев подобия.

При  создание модели возможно.