Другие предметы \ Моделирование объектов и систем управления отрасли

Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 10

4)   — период реализации случайного процесса. Погрешность определения спектральной плотности зависит от величины . Если принять погрешность приблизительно раной 2%, то  должно быть равно: . 

2.6.3  Определение динамических характеристик объектов и систем управления методом моментов

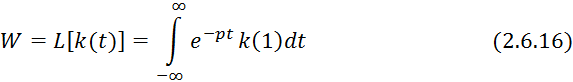
Разложим  в ряд Падэ:

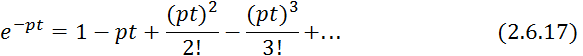
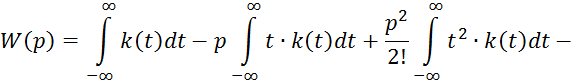
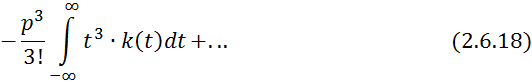
где  — момент -ого порядка импульсной функции.

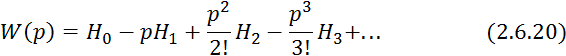
Момент  импульсной функции можно определить по моментам корреляционной и взаимокорреляционной функции следующим образом:

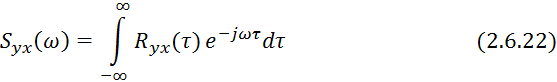
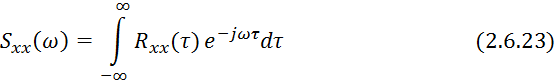
 — момент взаимокорреляционной функции:

 — момент корреляционной функции:

Подставим в 2.6.21; 2.6.22, 2.6.23, 2.6.20:

;

;

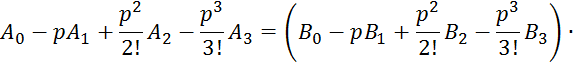
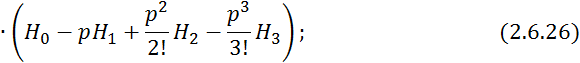
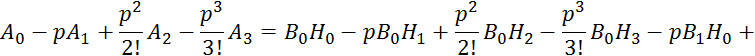
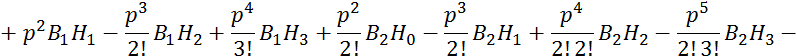
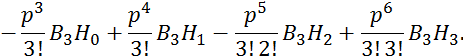
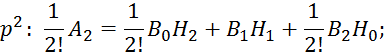
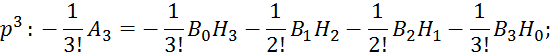
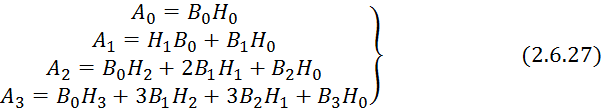
Так как корреляционная функция четная, то все моменты нечетного порядка будут равны 0. С учетом этого условия перепишем 2.6.27:

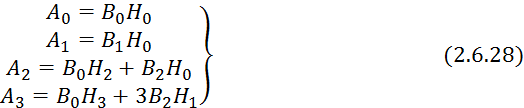
Так как .

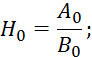
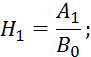
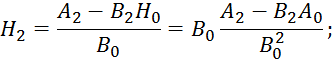
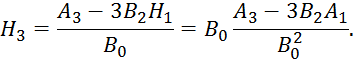
Если на входе системы действует случайный процесс в виде белого шума, то корреляционная функция определяется в виде -функции, то есть . Можно подобрать  таким образом, что , а . Поэтому система 2.6.28 примет вид:

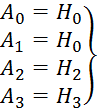
тогда:

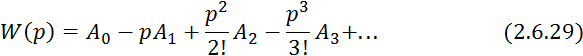
Данный метод моментов предполагает структуру искомой передаточной функции в виде бесконечного ряда моментов импульсной функции. На практике порядок искомой передаточной функции ограничен, поэтому понижается точность полученной передаточной функции. 

2.6.4  Применение метода модулирующих функций для определения динамических характеристик объектов и СУ

Данная задача решается в несколько этапов:

На первом этапе принимается и выбирается дифференциальное уравнение -ого прядка, описывающее динамические свойства моделируемого объекта.

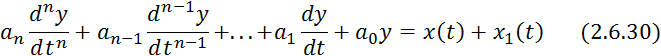
где  — входная переменная процесса;

 — шум.

Принимается, что  случайный процесс с математическим ожиданием равным нолю.

 — искомые коэффициенты.

На втором этапе выбирается моделирующая функции . Свойства:

1)  она должна быть непрерывной;

2)  она должна быть ограничена и дифференцируема;

3)  на границе интервала  сама функция и все её производные должны быть равны нолю.

Третий этап. Умножаем уравнение 2.6.30 на :

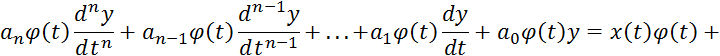
Для нахождения коэффициентов уравнения 2.6.31 проинтегрируем его по частям. При этом каждая составляющая интегрируется только раз каков порядок производной этой составляющей. В результате получим;

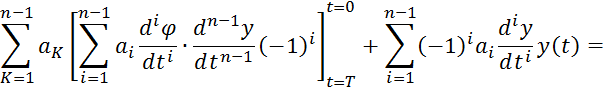
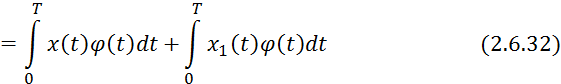
С учетом свойства модулирующих функций:

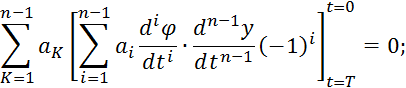
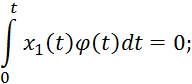
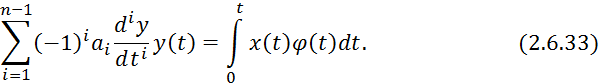
Для составления  уравнений необходимо составить реализацию  и  

В качестве примера моделирующей функции можно принять следующее выражение:

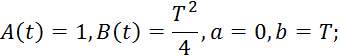
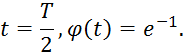
2.7.  Получение модели статики объектов и СУ

2.7.1  Определение моделей статики (уравнения регрессии) при пассивном эксперименте

Если при моделировании объекта с применением этого метода переменные   не могут контролироваться, то применяется статический метод.

Сущность: в режиме нормальной эксплуатации объекта измеряется входные переменные  и соответствующие им  (см. Таблицу 2.1).

При планировании опытов эксперимента необходимо учитывать предпосылки методов корреляционного и регрессионного анализа, которые применяются для обработки данных эксперимента для получения уравнения регрессии вида 2.5.2.

Предпосылками корреляционного анализа являются:

1)    и  являются случайными нормально распределенными величинами;

2)  Корреляционной связью между данными переменными является такая связь, при которой с изменением одной величины изменяется другая.

Предпосылками регрессионного анализа являются:

1)   Величина  является не случайной, а  — случайная нормально распределенная;

2)   Величины  измеренные в различных опытах должны быть независимы друг от друга. Эта независимость обеспечивается выбором интервала времени. Интервал времени спада корреляционной функции.

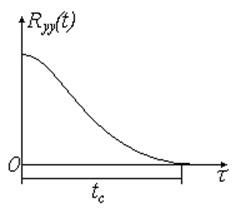
Рис. 14

3)    измеряется с погрешностью намного меньше чем величина ;

4)   Дисперсии  полученные в различных опытах должны быть одинаковыми. Для этого каждый опыт повторяется -раз и по результатам этих опытов рассчитывается дисперсия. Однородности дисперсий оценивается о применении статистических критериев.

Количество опытов , где -число входных переменных.

Для получения модели статики необходимо последовательно решить следующие задачи:

Скачать файл