Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 5

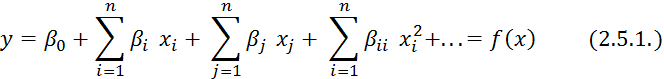
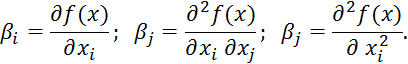
где , , ,  — теоретические коэффициенты полинома.

Данные полинома могут быть получены при бесконечном числе опытов и при отсутствии возмущающих воздействий.

В реальном ХТП всегда присутствует возмущающее воздействие, и количество опытов ограничено и называется выборкой. Поэтому полученная модель является оценкой соответствующего теоретического уравнения 2.5.1. и называется уравнением регрессии следующего вида:

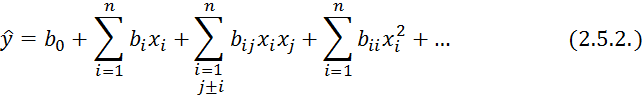
где  — приближенное значение;

, , , , — оценки соответствующих теоретических коэффициентов и называются коэффициентами уравнения регрессии;

 — свободный член;

 — линейный эффект (линейное влияние  на );

 — эффект попарного взаимодействия;

 — квадратичный эффект.

Данная полиномиальная форма 2.5.2. удобна и эффективна так как:

1)  увеличивается точность математического описания ХТП;

2)   она позволяет сравнительно просто определить коэффициенты уравнения с помощью ЭВМ.

2.5.2.  Модели динамики (статистические) химико-технологического процесса

А)   Основные виды возмущающих воздействий и основные виды получаемых моделей.

Для получения статистической модели динамики химико-технологического процесса (ХТП) создается испытательное возмущающее воздействие  и измеряется изменение  объекта . Полученное выражение  является решением с  в правой части с нулевыми начальными условиями . То есть подбирается такая аппроксимирующая функция (то есть решение дифференциального уравнения), которая совпадает с данной экспериментальной зависимостью . Точность получаемой модели зависит от точности аппроксимации  решение дифференциального уравнения.

По виду испытательных возмущений  различают пассивный и активный эксперимент. При пассивном в качестве  используются случайные функции входной координаты .

Экспериментальный метод получения модели динамики базируется на предположении сосредоточенности переменных, на линейности статической характеристики  и стационарности процесса. Это позволяет описать динамику процесса в виде однородного дифференциального уравнения.

ХТП являются процессами с распределенными параметрами. Данные ХТП могут быть представлены как объекты сосредоточенными параметрами, распределённость может быть учтена в модели звеном чистого запаздывания. При небольшом изменении входных переменных  можно принять зависимость линейной. Все ХТП являются нестационарными, но на интервале изменения данный ХТП является стационарным, так как динамические свойства меняются медленно.

Вывод: с учетом всех допущений динамическую модель ХТП можно представить в виде однородного дифференциального уравнения.

Динамическую модель можно представить в виде:

1)  однородными дифференциальными уравнениями

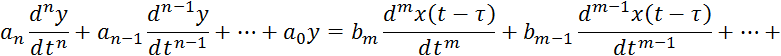
где   — чистое запаздывание.

2)  передаточными функциями

3)  амплитудно-фазовыми характеристиками

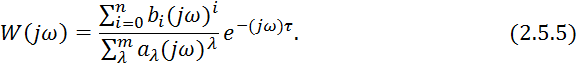
2.5.3.  Определение динамических характеристик химико-технологических процессов при активном эксперименте

Основным методом является метод переходных функций. Переходной функцией  называется зависимость выходной координаты  при изменении входной координаты от значения  до .

где  — значение входной координаты в стационарном режиме.

Функция  задается в виде графика или таблицы. Если статическая характеристика объекта линейна, то также являются линейными и их величина не влияет на динамику объекта, то есть

Если входная координата -функция:

то выходная координата 𝛿 имеет вид импульсной функции

Активный эксперимент для получения динамической характеристики химико-технологического процесса (ХТП) заключается в снятии функции  и аппроксимацией её решением однородного дифференциального уравнения с постоянными коэффициентами и нулевыми начальными условиями.

Процесс определения динамических характеристик включает:

1)  Изучение промышленного объекта моделирования. Для этого изучается технология процесса, КИПиА, исследуется сам процесс ХТП как объект управления и в результате составляется следующая схема:    

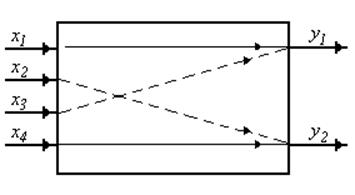
Рис. 6 Схема исследуемого объекта