Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 29

Задача оптимизации ставится следующим образом:

Для решения задачи оптимизации в данной постановке на первом этапе составляется вспомогательная функция :

где   — неопределенный множитель Лагранжа.

На втором этапе составляется система уравнений:

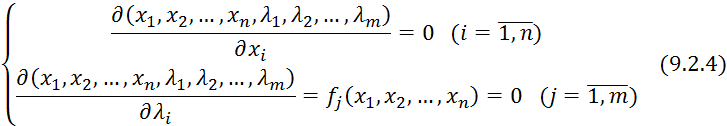
В процессе вычисления  множитель Лагранжа   имеет вспомогательное значение, а сами исключаются из конечного решения системы.  

9.3.3.  Линейное программирование

Они применяются для оптимизации, если сама целевая функция и ограничительная функция имеют линейную форму. При этом ограничительная функция задается в виде неравенств:

Задача оптимизации решается шаговым или симплекс методом.

 — прямая линия.

Совокупность ограничительных линий для   представляет собой многогранник. При поиске максимума функции  внутри данного многогранника перемещается параллельно самой себе линия. Оптимум данной функции находится или в вершине многогранника или совпадает с одной его гранью.

9.3.4.  Нелинейное программирование

Метод охватывает большой круг методик. Среди них применяется градиентный метод оптимизации. Для нахождения максимума — метод крутого схождения, для минимуму — метод наискорейшего спуска.

Градиентный метод относится к поисковым методам. Эти методы хорошо приспособлены для решения задач на ЭВМ.

В общем случае целевая нелинейная функция определяется в виде:

Определяется значение  вызывающим наибольшим изменением функции . Это достигается при движении вдоль градиента ортогональной и контурной поверхности данной функции , то есть к контуру, где  в некоторых точках .

Данные методы отличаются друг от друга способом определения направления градиента, величиной шага, длительностью движения, критерием окончания поиска.

Градиентом 9.2.7 будет:

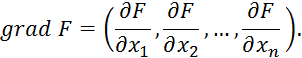
где  — пропорционально косинусу угла между направлением градиента к оси .

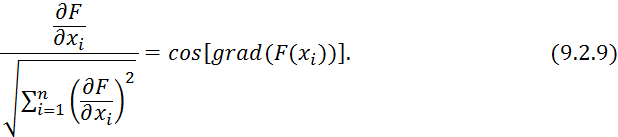
Выбор величины шага. Шаг должен быть не очень малым и не очень большим. Величина шага определяется частной производной в исходной базисной, то есть;

где  — коэффициент пропорциональности, определяющий шаг по всем координатным осям.

Общий алгоритм градиентного метода.

Данный алгоритм 9.2.10 и 9.2.11 показывают только направление вектора градиента, не учитывает скорость изменения данного градиента. С учетом этого алгоритм изменяется и имеет вид:

Величина шага 9.2.12 изменяется при приближении к экстремуму. При этом согласно 9.2.12 направление градиента зависит от базисной точки на поверхности функции .

Таким образом, методика применения градиентных методов выполняется в следующие этапы:

1)  Выбирается базисная, то есть исходная точка;

2)  Определяется направление градиента;

3)  Определяется величина шага по данному градиенту;

4)  Определяется последующая точка поиска:

5)  Сравнивается значение целевой функции с предыдущей, и если её значение больше чем предыдущей, то делается следующий шаг; если целевая функция на последующем шаге меньше чем на предыдущем, то выбираем новое направление градиента.

Критерием окончания поиска является достижением такой точки, при движении которой по любой координатной оси не достигается значения целевой функции.

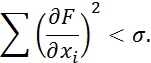
где  — погрешность вычисления.

9.4.  Численные методы оптимизации. Постановка задачи оптимизации 

Целевая функция  является не модельной, то есть имеет один  экстремум. Примем за экстремум её максимальное значение.

То есть программу поиска применять, изменяя знак на обратный.

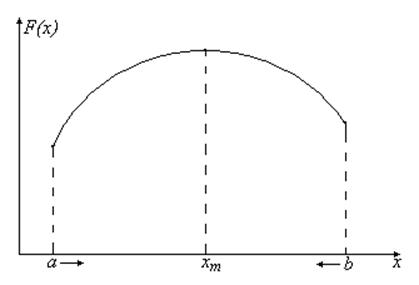
Рис. 50

Сущность численных методов заключается в локализации области близкой к экстремуму, а затем уточнение в данной области величиной .

Численные методы классифицируются на следующие:

1)  Метод равномерного поиска;

2)  Метод поразрядного приближения;

3)  Метод квадратичной интерполяции;

4)  Метод дихотомии;

5)  Метод “золотого сечения” и др..

А)   Метод равномерного поиска.

Сущность. Переменной  присваивается значение :

1)  ;