Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 23

 — скорость стадии -той реакции.

По закону действующих масс:

где   — константа скорости -той реакции;

 — концентрации.

Общий порядок реакции равен;

где   зависит от температуры:

где   — предэкспоненциальный множитель, зависящий от свойств компонентов;

 — энергия активации -той реакции;

Химические реакции по количеству стехиометрических уравнений описывающих их протекание подразделяются на простые и сложные.

Пример простых:

1)   

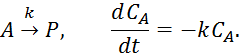
2)   

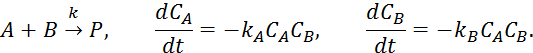
3)   

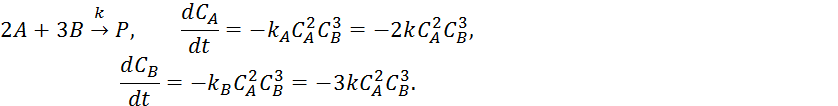
Константы скорости реакции по соответствующему компоненту равна константе стадии реакции  на соответствующий стехиометрический коэффициент.

Сложные реакции делятся на параллельные, последовательные и смешанные и обратимые. Изменение концентрации -того вещества в сложной реакции равна скорости его образования (расходования) на всех стадиях в которых данное вещество участвует, то есть сложная реакция разделяется на отдельные стадии.

Пример:

1)  Параллельная реакция:

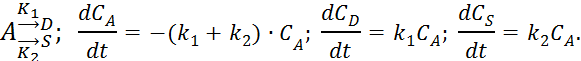
2)  Последовательная реакция:

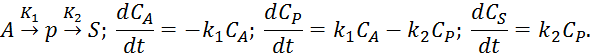
3)  Обратимая реакция:

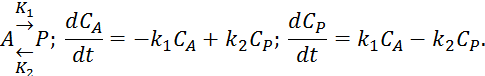
4)  Смешанная:

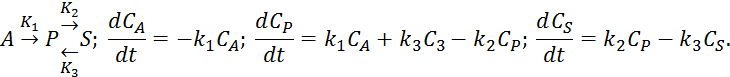
6.2.  Математическая модель химического реактора идеального перемешивания

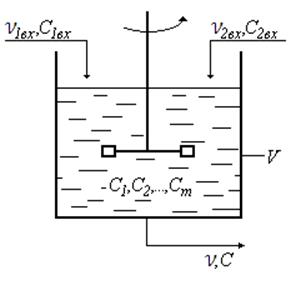
Рис. 36

Вследствие идеального перемешивания концентрация всех компонентов на входе из реактора постоянна.

 — плотность всех компонентов поступающих в реактор;

 — плотность в реакторе;

 — объем зоны идеального перемешивания.

Математическая модель включает уравнение материального баланса по жидкой фазе и по концентрациям каждого -ого компонента.

Материальный баланс по жидкой фазе:

Уравнение материального баланса по изменению -ого компонента:

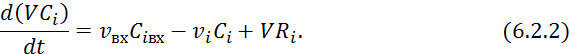
где   — скорость реакции по -ому компоненту;

 равно сумме скоростей образования и расходования  -ого компонента.

Пусть в реакторе протекает  реакций:

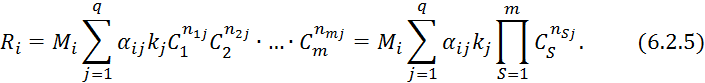
Подставляем 6.2.2 в 6.2.5:

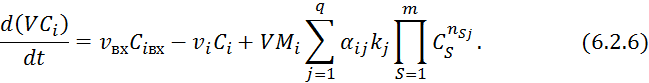
Пример:

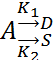
Принимаем, что

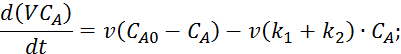
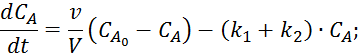
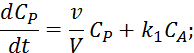
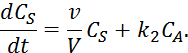
6.3.  Математическая модель реактора идеального вытеснения

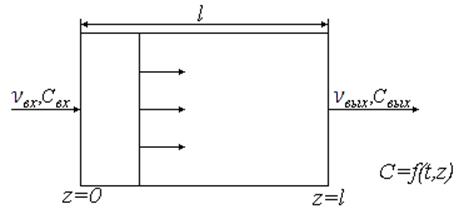
Рис. 37

Математическая модель включает уравнение по потокам  и по концентрациям компонентов веществ участвующих реакциях.

Уравнение материального баланса по потокам вещества согласно разделу 3.4 имеет вид:

Изменение концентрации -того вещества определяется двумя факторами:

1)  Гидродинамикой процесса;

2)  Скоростью химического превращения.

Уравнение материального баланса по измерению концентрации -того вещества имеет следующий вид:

Вместо  подставляем 6.2.5:

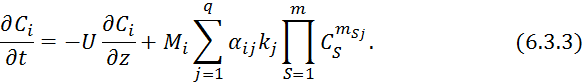
Пример:

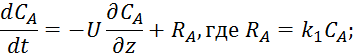
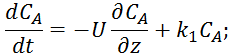
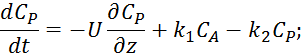
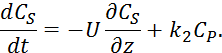
6.4.  Передаточные функции химических реакторов

6.4.1.  Передаточная функция реактора идеального перемешивания простого типа

где  — концентрация исходного вещества.

Уравнение материального баланса по компоненте :

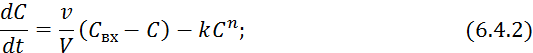
Принимаем :

где  — концентрация в любой точке;

 — оператор.

Так как начальные условия не нулевые то оператор  является нелинейным.

Для решения 6.4.4 оператор  необходимо привести к линейной форме:

где  — линейный оператор;

Преобразуем 6.4.4:

Рассмотрим 6.4.7 при :

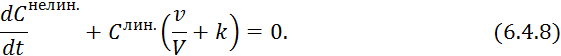
где  — результат действия нелинейного оператора  при .

Решение уравнения 6.4.8 при 6.4.9 будет иметь следующий вид:

Вычитаем из уравнения 6.4.7 уравнение 6.4.8:

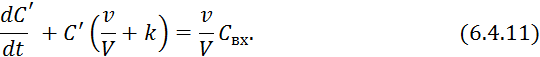
где

Преобразуем по Лапласу по времени при начальных условиях 6.4.12 уравнение 6.4.11:

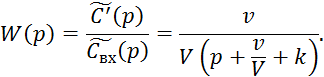
6.4.2.  Реактор идеального вытеснения

где  — концентрация вещества .

Уравнение модели реактора будет иметь следующий вид:

Перепишем 6.4.16 с условием 6.4.20:

Преобразуем по Лапласу по времени 6.4.21 при нулевых начальных условиях:

 

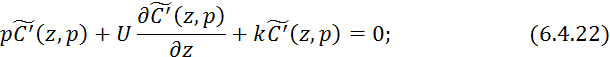
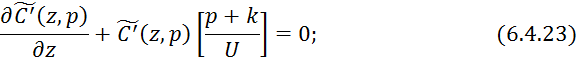
Решение уравнения 6.4.23 с граничными условиями 6.4.24:

)

Уравнение 6.4.25 при  примет вид:

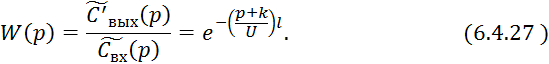
7.  Математическое моделирование динамики типовых контуров регулирования технологических параметров объекта

7.1.  Свойства, характеристики и классификация объектов регулирования

Свойства объекта регулирования определяют выбор типа регулятора для контура объекта, расчет настроек регулятора, а также является основой синтеза автоматической системы регулирования (АСР).

Основными свойствами являются:

1)  самовыравнивание;

2)  емкость;

3)  запаздывание.