Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 8

А)   Аппроксимация переходных функций решением дифференциальных уравнений с простыми действительными корнями.

Этот метод применяется для переходных функций имеющих неколебательный характер, при этом  может быть представлено решением линейного дифференциального уравнения:

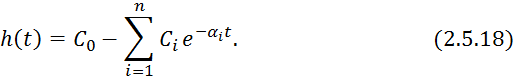
где  — значение переходной функции при установившемся значении;

 — постоянная интегрирования;

 — кони и полюса, .

При этом:

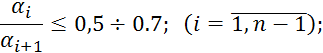
Необходимо найти ,,.

Сущность метода заключается в последовательном приближении  решением однородного дифференциального уравнения первого порядка, то есть нахождением величины  и если данное решение будет не удовлетворительно на интервале , то порядок уравнения увеличивается, и получаем  и т.д..

Величины , на каждом этапе аппроксимации определяется методом последовательного логарифмирования функции.

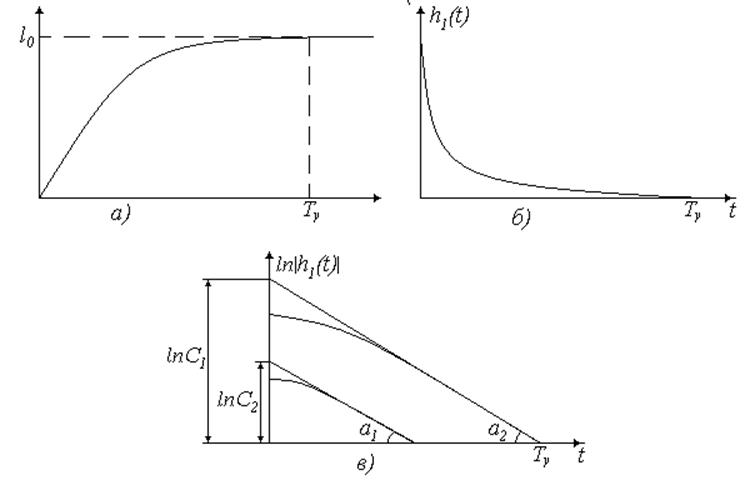
Рис. 8 Аппроксимация переходной функции дифференциальным уравнением

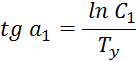
Если на всем отрезке времени  касательная совпадает с логарифмической кривой, то качество аппроксимации удовлетворительно и можно ограничиться приближением первого порядка, если не удовлетворительно, то вводим :

Данный метод продолжается до тех пор, пока  при точности 1÷2%.

Практика применения данного метода показала, что переходную функцию можно аппроксимировать до четвертого порядка.

Правильность нахождения , определяется соотношениями:

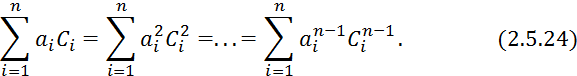
Эти равенства выполнить довольно затруднительно, так как нахождение , связано с погрешностями при графическом построении.

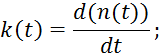
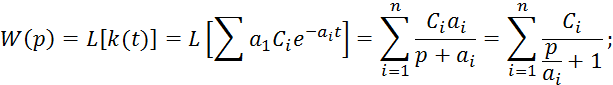
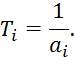
В)   Определение коэффициентов передаточной функции по экспериментальной переходной функции методом площадей.

Требуется по графически или таблично заданной  определить коэффициенты  передаточной функции.

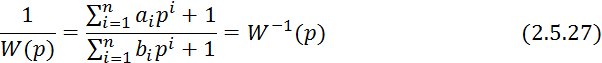
пусть n=3

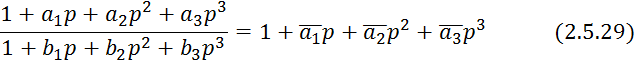
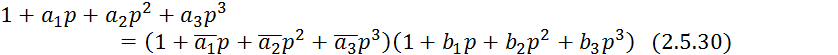
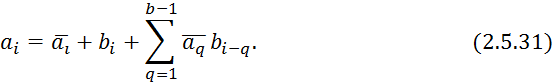
Необходимо найти разложение . Нахождение выполняется следующим образов:

Предположим, что исходная передаточная функция имеет первый порядок ( ), то есть необходимо найти только коэффициент , для его нахождения вычисляется площадь ограниченная кривой , где  — коэффициент передачи, а

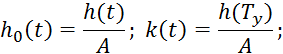
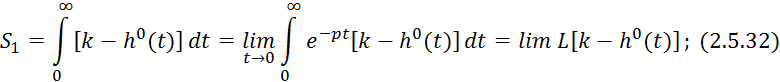
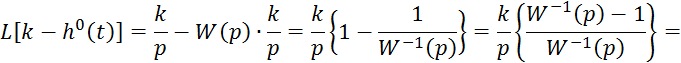
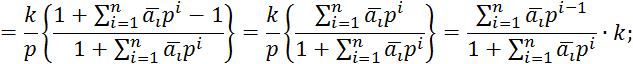
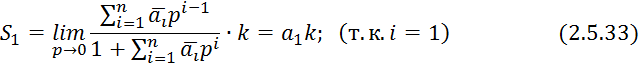
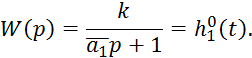
Преобразуем по Лапласу :

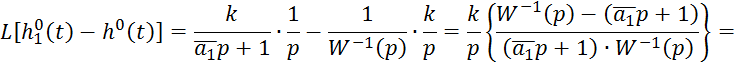
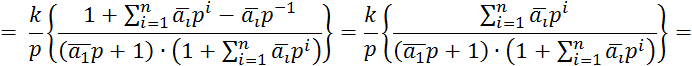
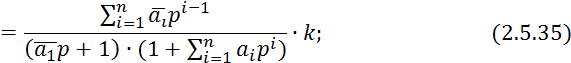
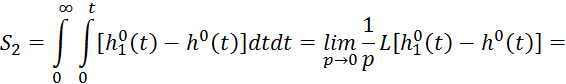
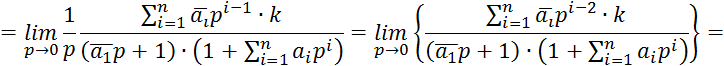
Зависимость 2.5.37 сложна, так как  осуществляет приблизительное интегрирование, при этом накапливаются ошибки, поэтому для вычисления площадей  применяется следующая формула, которая является преобразованием формулы 2.5.37:

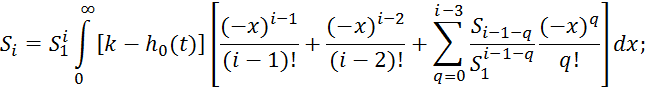
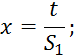
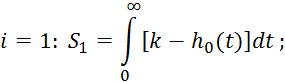
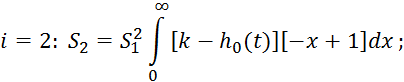
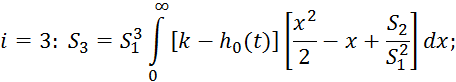
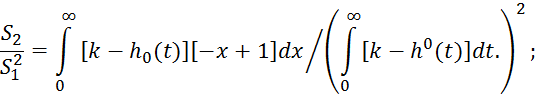
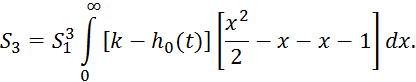
Данный метод не накладывает ограничений на порядок искомой передаточной функции. Выражение 2.5.28 может расходиться, что имеет место при значениях  Поэтому при применении формулы 2.5.37 необходимо заранее предположить, что  тогда мы получим сходящийся ряд (2.5.28) и коэффициенты  можно принят =0.

Порядок передаточной функции определяется по величинам рассчитанных площадей . Если на каком-либо этапе , то применяем порядок передаточной функции . Если  на каком-либо этапе расчёта меньше 0, то порядок передаточной функции принимается  и увеличивается порядок числителя, то есть вводится .   

Коэффициент передаточной функции 2.5.26 вычисляется с помощью системы уравнений 2.5.31.  

C)   Аппроксимация передаточных функций решением дифференциального уравнения первого порядка с запаздыванием.

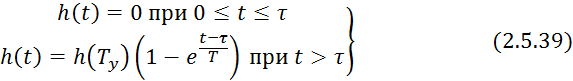
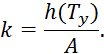
где   — амплитуда периодического возмущающего колебания.

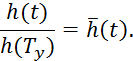
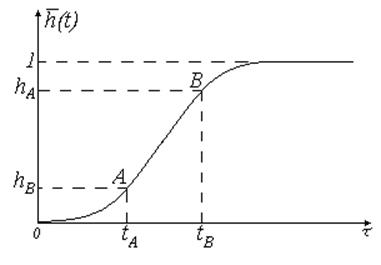
Рис. 9 Вид интерполяционной кривой

Интерполяционная кривая имеет четыре общие точки: , и установившееся значение.

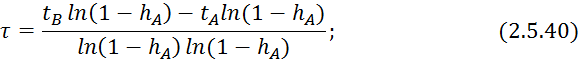
D)   Аппроксимация передаточных функций объектов содержащих интегрирующие звенья.

При заданном входном апериодическом воздействии  по виду передаточной функции можно определить наличие интегрирующих звеньев при математическом описании объекта.

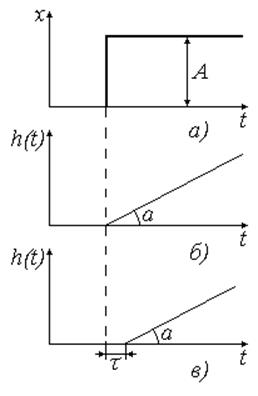
Рис. 10

Для Рис. 10 б) получаем следующие зависимости:

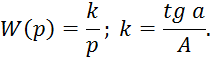
Для Рис. 10 в) получаем следующую зависимость:

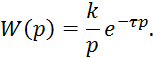
Рассмотрим более общий  случай

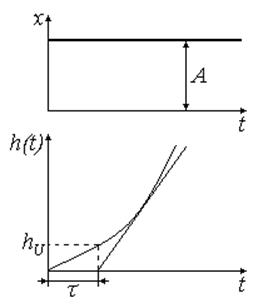
Рис. 11

Для Рис. 10 получаем следующие зависимости:

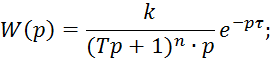
2.6.  Определение динамических характеристик объектов при входных воздействиях в виде случайных сигналов

В промышленных условиях несение апериодических активных воздействий нежелательно. Поэтому динамические характеристики можно получить только с использованием случайных сигналов на входе и на выходе данных объектов. При этом задача моделирования осуществляется в два этапа: