Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 16

Предположим, что наихудшая точка это :

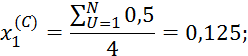
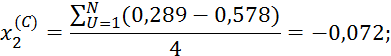
Получаем симплекс , , , .

Достоинства симплекс-планирования:

1)  Значительно меньшее количество опытов планирования по сравнению с ортогональными планами первого прядка;

2)   Введение в программу эксперимента дополнительного фактора  число опытов увеличивает на единицу, в то ж время как в методе ортогонального планирования первого полрядка число опытов увеличивается в два раза;

3)   Продвижение к оптимуму может вестись по нескольким выходным координатам;

4)  Переменные  и  могут измеряться с некоторой погрешностью.

Недостаток:

1)  Невысокая точность получаемого уравнения регрессии.

Все рассмотренные активные эксперименты относятся к числу лабораторных или полупромышленных.  

Е)   Эволюционное планирование эксперимента (EVOP).

Данный эксперимент прм6еняется в промышленности для моделирования крупнотоннажных действующих химико-технологических процессах (ХТП).

Входные переменные  могут варьироваться в небольших пределах. Кроме того, на действующий процесс влияют помехи, которые создают шумовое поле на выходе ХТП, то есть это вызывает погрешности в измерении выходных перемещений , то есть помехи вносят вклад в измерении . Задача заключается в выделении полезных сигналов на данном шумовом поле, это означает, что необходимо определить зависимости  от варьируемых : .

Для решения данной задачи применяется метод накопления и усреднения ошибок: погрешность средней величины  за  измерений в  раз меньше ошибки единичного измерения.

EVOP состоит из отдельных фаз, каждая из которых представляет собой ПФЭ или ДФЭ, который повторяется  раз.

По результатам проведения первой фазы эксперимента определяется условие проведения, последующей фазы по следующим вариантам:

1)  За центр плана последующей фазы применяется наилучшее значение ;

2)  Изменяется интервал варьирования ;

3)  Стабилизируется на некотором оптимальном уровне входные переменные предыдущей фазы и в рассмотрение вводят новые .  

Пример:  

 — время пребывания:

 — выход продукта.

Проводим ПФЭ=2²=4 опыта.

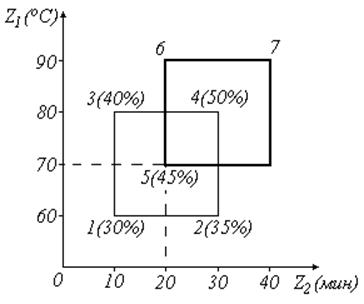
Рис. 17

 

 

После проведения каждой фазы рассчитывается эффект среднего:

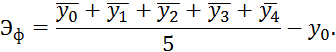
Если  является незначительной величиной, то эксперимент проводится вдали от среднего.

Если  является значительной и отрицательной, от эксперимент проводится вблизи максимума.

Принимаем за центр второй фазы наилучшую точку, то есть точку номер 4.

3.  Детерминированные (аналитические) модели химико-технологических процессов

3.1.  Использование уравнений материального и теплового баланса для описания стационарных и нестационарных режимов протекания химико-технологических процессов

Согласно блочному принципу разработки математических моделей сложных химико-технологических процессов (ХТП) исследуются и моделируются элементарные процессы (блоки) протекающие на различных уровнях ХТП.

В основе математического описания протекания данных элементарных процессов лежат уравнения материального и теплового баланса. 

Обобщенное уравнение материального баланса:

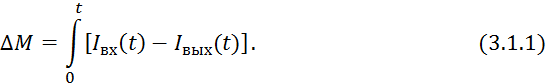
где  — накопление вещества за время [0,t];

 — входной и выходной потоки.

Данное уравнение описывает нестационарный режим работа ХТП. Стационарный режим описывается уравнением материального баланса:

(приход вещества)=(расходу вещества)

Аналогичные уравнения можно записать для теплового баланса:

(приход тепла)-(расход тепла)=(накопление тепла)

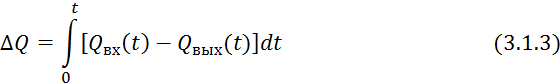
где  — изменение энтальпии объекта за время [0,t];

 — входной и выходной потоки.

Уравнение 3.1.3 описывает нестационарный режим работы ХТП.

Стационарный режим описывается:

Приведенные уравнения описывают элементарные процессы, протекающие на макроуровне.

Для описания стационарных режимов применяются конечные уравнения и их системы. Для описания нестационарных режимов применяется однородные дифференциальные уравнения (линейные и нелинейные) и их системы, дифференциальные уравнения в частных производных.

3.2.  Модели структуры потоков, как основа построения математических моделей гидромеханики химико-технологического процесса