Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 14

Пример:

, ;

ДФЭ вида , который представляет собой половину ПФЭ называется полурепликой.

Применяется также ДФЭ вида  и называются четвертой репликой.

Достоинства ПФЭ и ДФЭ состоят в следующем:

1)  Коэффициенты уравнения регрессии  определяются независимо друг от друга по простым формулам;

2)   для всех коэффициентов уравнения регрессии одинаков и минимален;

Недостаток ДФЭ — невысокая точность получаемого уравнения регрессии, так как коэффициенты являются смешанными оценками.

В)   Описание почти стационарной области

То есть эта область близкая к экстремальному значению  представляющее собой куполообразную форму. Для описания данной области необходимо применить нелинейные уравнения регрессии в которых значимыми являются квадратичные члены.

Методика:

1)  Проводится ПФЭ

вычислим свободный член

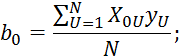
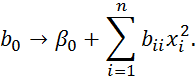
Приводится эксперимент в центре  и находим :

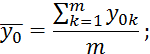
Если это соотношение является значимым, тогда это означает, что в данной области факторного пространства является значимыми квадратичные коэффициенты.

Для получения уравнений регрессии необходимо переменные  варьировать как минимум на трех уравнениях:

Таблица 2.8

Для уменьшения количества опытов Бокс и Уилсон предложили композиционные или последовательные планы. Ядро этого плана:

1.1  ПФЭ= для ;

1.2  ДФЭ= для .

2)  Если полученное уравнение регрессии по данному плану является неадекватным то проводится дополнительное количество опытов в так называемых “звездных точках”:

где  — звездное плечо—это расстояние от центра плана до данной звездной точки.

1)    Проводится эксперимент в центре плана   .

Общее количество опытов в данном плане

Пример:

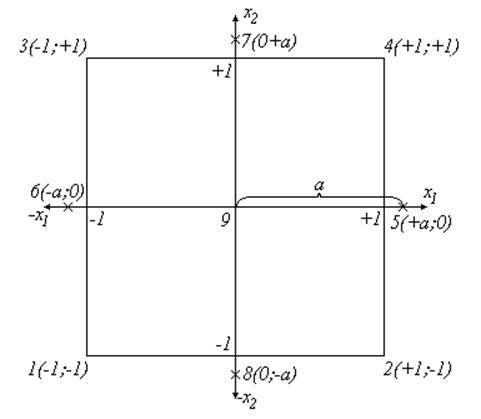
Рис. 15

Таблица 2.9

№
1	+1	-1	-1	+1	1	1
2	+1	+1	-1	-1	1	1
3	+1	-1	+1	-1	1	1
4	+1	+1	+1	+1	1	1
5	+1	+	0	0		0
6	+1		0	0		0
7	+1	0	+	0	0
8	+1	0		0	0
9	+1	0	0	0	0	0

Рассмотрим свойства композиционного плана (Таблица 2.9):

1)   

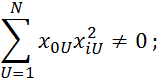
2)   

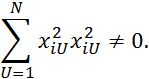
То есть данная матрица (Таблица 2.9) не ортогональна. Её можно привести к ортогональному виду используя следующие методы:

1)  Замена квадратичных столбцов линейными преобразованными переменными:

.

2)  Выбор соответствующей величины звездного плена  зависящего от числа :

Г)   Ортогональный план второго порядка.

Преобразование квадратичных элементов столбцов в линейные элементы производится по следующему соотношению:

1)   

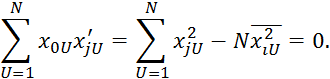
2)   

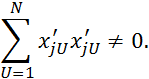
Для окончания приведения матрицы (Таблица 2.9) необходимо произвести выбор звездного плеча  таким образом, чтобы обратная матрица  была диагональной:

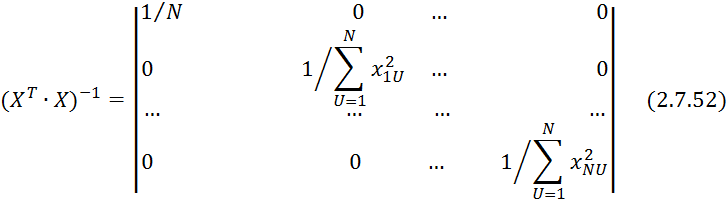
Для определения величины  для выполнения условия 2.7.52 величина  будет иметь следующие значения:

Таблица 2.10

С учетом зависимости 2.7.51 и данных Таблицы 2.10 матрица будет ортогональной (Таблица 2.11):

Таблица 2.10