Алгоритмы ПАИАМ могут решать существенно более сложные задачи, чем БАИАМ. Общая структура ПАИАМ процесса. Для оптимизации химико-технологического процесса (ХТП) необходимо выбрать критерий, который отражает технологическую цель. Критерий может быть экономическим или технологическим. На основании выбранного критерия составляется целевая функция и ограничительная функция.
Ограничительная функция — зависимость показателей ХТП от параметров, влияющих на их значение.
При этом в целевую и ограничительную функции включается одинаковые аргументы. Задача оптимизации решается в том случае, если необходимо преимущественное улучшение показателей работы ХТП балансируя один (или второй) показатель против другого (или первого).
Любой ХТП по формальным признакам, действующим на него параметров можно представить следующей схемой.
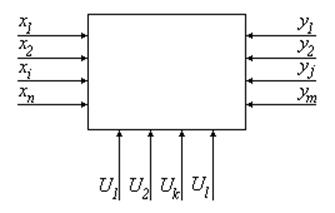
Рис. 49
где
![]() — входные контролируемые параметры;
— входные контролируемые параметры;
![]() — управляемые параметры:
— управляемые параметры:
![]() — выходные параметры, которые являются суммарным
действием входных и управляемых параметров.
— выходные параметры, которые являются суммарным
действием входных и управляемых параметров.
Параметры представим в векторной форме:
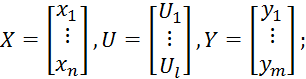
![]()
Выражение 9.1.1 — математическая модель данного ХТП.
![]()
Выражение 9.1.2 — система уравнений данной математической модели.
![]() с
учетом 9.1.1 получим:
с
учетом 9.1.1 получим:
![]()
Решение задачи
оптимизации представляется в виде зависимости управляющих воздействий от
вектора пространственных координат ![]() :
:
![]()
Для каждого ![]() необходимо
найти такой вектор
необходимо
найти такой вектор ![]() , который обеспечит экстремум критерия
, который обеспечит экстремум критерия ![]() . Решение
возможно только при наличии математической модели.
. Решение
возможно только при наличии математической модели.
Различают две
стадии оптимизации: статическая и динамическая. Статическая заключается в
определении нового наилучшего состояния объекта, если это вызывается
необходимостью при изменении вектора входных параметров ![]() .
.
Статическая оптимизация заключается в переводе объекта из одного установившегося состояния в другое.
Критерий оптимизации в этом случае может быть;
Без
ограничения: ![]()
С
ограничениями: 
Решение задачи оптимизации будем иметь в виде:
![]()
Статическая
оптимизация применяется для оптимального управления такими непрерывными
процессами, которые при определенном значении ![]() достигают
установившегося значения за приемлемый промежуток времени.
достигают
установившегося значения за приемлемый промежуток времени.
Существует ряд процессов, которые характеризуются нестационарным режимом протекания процесса, который описывается динамическим выражением — динамическая оптимизация. Примеры: все периодические процессы химической технологии; критерий: за один цикл получить продукт максимального качества за минимальное время.
В данном случае функция оптимальности является критерием времени, который должен учитывать поведение объекта в течении всего периода нестационарной работы. Поэтому критерий оптимизации имеет интегральную форму;

![]()
Задача динамической оптимизации решается следующим образом:
для каждого
момента времени ![]() для любого значения вектора входных
для любого значения вектора входных ![]() определяется
вектор управляющих параметров
определяется
вектор управляющих параметров ![]() , который обеспечивает оптимальное поведение объекта
, который обеспечивает оптимальное поведение объекта
![]()
Выбор метода
оптимизации (поиска ![]() ) зависит от постановки задачи и от вида
математической модели. Для оптимизации применяются аналитические и численные
методы.
) зависит от постановки задачи и от вида
математической модели. Для оптимизации применяются аналитические и численные
методы.
9.3. Аналитические методы оптимизации
Они классифицируются на следующие виды:
1) Метод классического анализа функций;
2) Метод неопределенных множителей Лагранжа;
3) Метод линейного программирования;
4) Метод нелинейного программирования;
5) Метод динамического программирования и др..
9.3.1. Метод классического анализа функций
Целевая
функция выходного переменного ![]() .
.
![]()
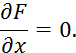
Для определения вида экстремума необходимо получить вторую производную:
![]()
![]()
![]()
Необходимо исследовать старшие производные. И если производная имеет четный порядок, то экстремум имеется, если не четный, то экстремума нет.
Пример: найти экстремум функции двух переменных:
![]()
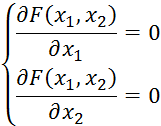
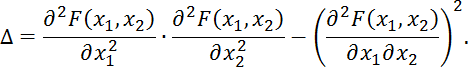
Если ![]() , то экстремум имеется, если
, то экстремум имеется, если ![]() , то экстремум отсутствует.
, то экстремум отсутствует.
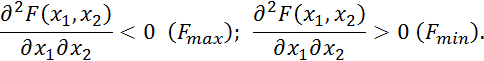
9.3.2. Метод неопределенных множителей Лагранжа
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.