Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 11

1.   Определить форму или вид уравнения регрессии 2.5.2;

2.   Рассчитать коэффициенты уравнения регрессии ;

3.   Определить силу связей между , ;

4.   Определить значимость ;

5.   Определить адекватность полученного уравнения регрессии от экспериментальных данных.       

А)  Определение вида уравнения регрессии.

Для каждой зависимости  принимается линейная форма уравнения регрессии:

и далее решаются все остальные задачи. Если принятая форма 2.7.1 является адекватной, то принятая гипотеза является удачной.

Б)   Определение коэффициентов уравнения регрессии:

Если 2.7.2 дифференцируема, то коэффициенты  можно определить с помощью метода наименьших квадратов, математическая формулировка которого имеет вид:

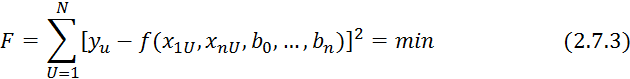
Данный функционал обеспечивает минимум квадрата разности между измеренным и рассчитанным значением выходной величины.

Для получения минимума необходимо:

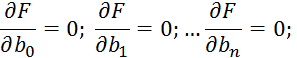
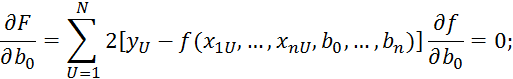
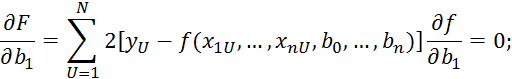
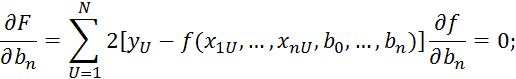
Преобразуем:

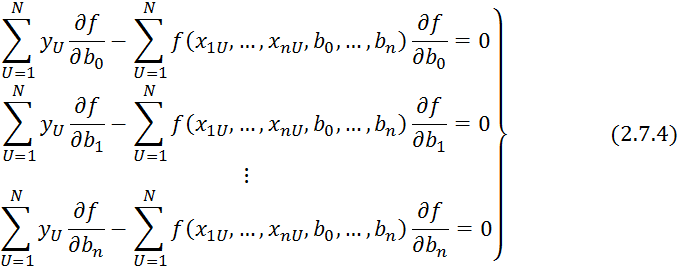
2.7.4 является системой нормальных уравнений.

В общем виде данная система не решается.

Пример1.

принимаем

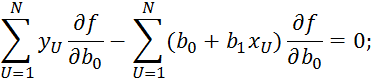
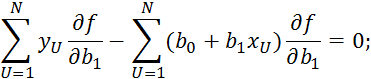
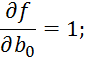
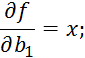
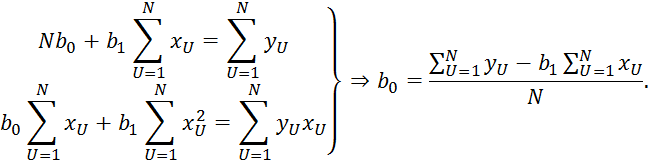
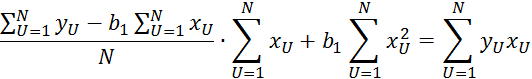
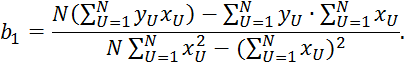
Пример 2.

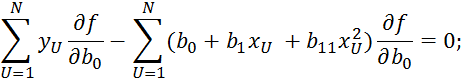
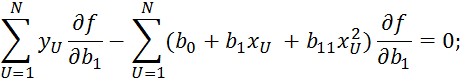
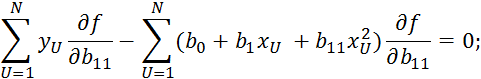
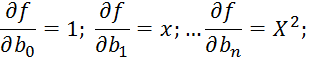
Пример 2. Трансцендентное уравнение регрессии.

В некоторых случаях при получении уравнения статики при малом числе опытов для получения адекватного уравнения полиномиальная форма недостаточна и применяется трансцендентные уравнения:

Для получения коэффициентов, чтобы получить систему нормальных уравнений необходимо линеаризовать уравнения 1, 2, 3.

Уравнения 1, 2 приводим к линейному виду путем логарифмирования:

   

В)  Определение силы линейной связи между , .

Для оценки силы связи применяется выборочный коэффициент корреляции:

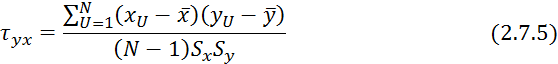
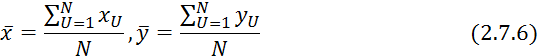
 — среднее квадратичное отклонение входной переменной.

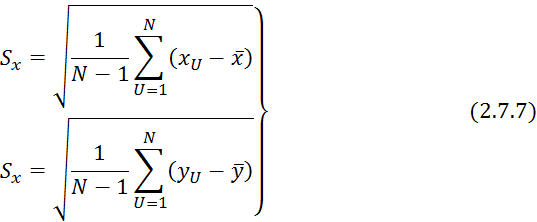
Чем выше по модулю значение , тем теснее связь между  и . Знак при  показывает на характер изменения  и : “+”  и  изменяются в одинаковом направлении.

Выборочный коэффициент корреляции, рассчитанный по 2.7.5 проверяется на значимости по следующей формуле:

 табличное значение критерия Стьюдента, которое выбирается из таблиц распределения Стьюдента для уровня значимости  и число степеней свободы .

Если неравенство 2.7.8 выполняется, то коэффициент  является статически значимым м между  и  существует линейная связь.

2.7.2  Регрессионный анализ в матричной форме

Для решения задачи получения уравнения регрессии с применением ЭВМ удобно производить вычисления в матричной форме.

 фиктивная величина.

Результаты пассивного эксперимента представим в форме:

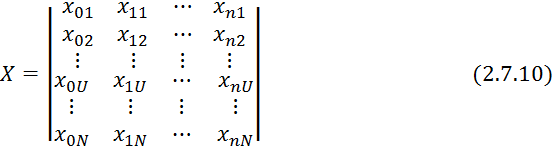
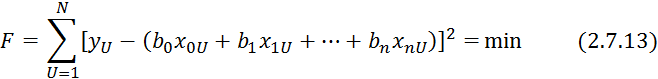
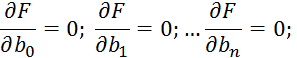
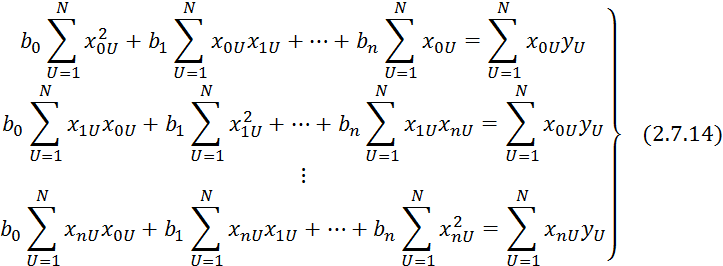
Решением 2.7.14 в матричной форме.

Транспонируем 2.7.10:

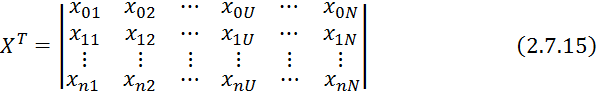
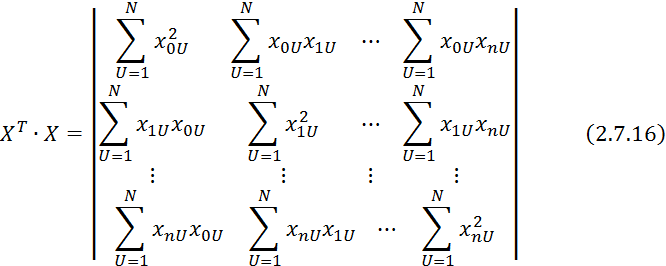
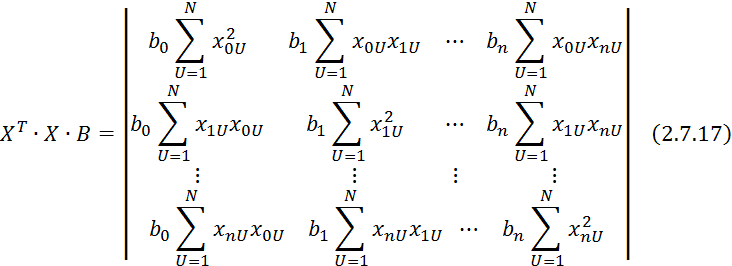
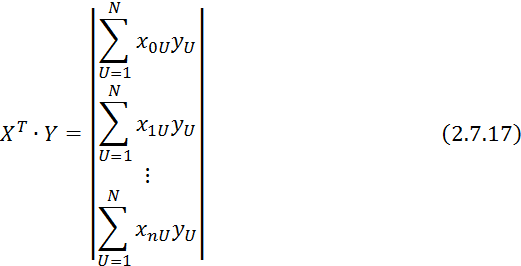
Домножим 2.7.19 на

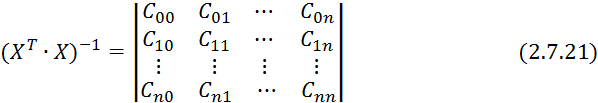
где — алгебраическое дополнение любого элемента матрицы ;

 — определитель матрицы 2.7.16.

Г)  Оценка значимости полученных коэффициентов  выполняется по следующему неравенству.

или , где  

 — среднеквадратичное отклонение коэффициента :

где  — соответствующий диагональный элемент обратной матрицы 2.7.21.

 —среднеквадратичное отклонение выходной величины  (см. формулу 2.7.7).

 — табличное значение критерия Стьюдента для  и .

Для всех  рассчитывается величина  и далее по выражению 2.7.24 производится оценка значимости . Если неравенство выполняется, то  является значимым и наоборот. Если несколько коэффициентов  не соответствуют неравенству 2.7.24, то вначале считается коэффициент незначимых  для которого  было наименьшим; данный параметр  исключается из матрицы исходных данных, а все остальные коэффициенты  пересчитываются заново, так как переменные  связаны между собой корреляционной связью.

Данная процедура проводится до тех пор, пока все  будут значимые.      

Д)  Проверка адекватности уравнения 2.7.9.

Для оценки используется неравенство:

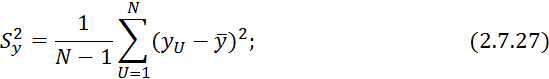
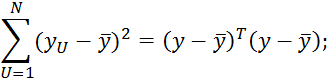
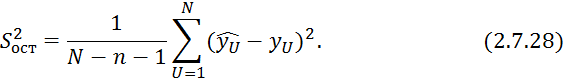
где   — расчетное значение выходной величины для условий -того опыта.

 — фактическое значение.

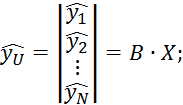
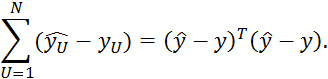
 — табличное значение критерия Фишера, которое выбирается из таблиц при  и числе степеней свободы числителя  уравнения 2.7.26  и   — числе степеней свободы знаменателя .

Если неравенство 2.7.26 выполняется, то полученное уравнение 2.7.9 является адекватным.

Если неравенство 2.7.26 на выполняется, то полученное уравнение регрессии  2.7.9 является неадекватным.