Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 12

2.7.3  Получение модели статики при активном эксперименте

Активный эксперимент проводится по заранее составленному плану при этом одновременно варьируются все , что дает возможность сохранить число опытов по сравнению с пассивным. Каждому активному эксперименту соответствует вид регрессии.

Для получения линейных уравнений регрессии применяются ортогональный метод первого порядка (симплекс планирование, дробный и т.д.).

Для получения нелинейных уравнений регрессии применяется ортогональный план второго порядка, центральные композиционные планы, рототабельные методы, -оплимальные планы и др.

А)   Полный факторный эксперимент (ПФЭ).

В данном эксперименте переменные  принимают два значения, при этом реализуется  всевозможные комбинации из  переменных на двух уровнях, то такой эксперимент называется ПФЭ.

.

Пример: предположим, что для некоторого объекта изучается влияние трех переменных:

 (температура)

 (давление)

 (время пребывание)

Выходной параметр — выход конечного продукта .

 

Среднее значение:  

Интервал варьирования:

Применение переменные  в безразмерный масштаб:

.

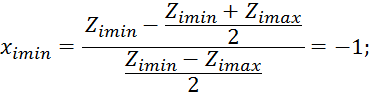
Количество опытов:

Составим матрицу:

Таблица 2.3

№	,	,	,				, %
1	100	2	10	-1	-1	-1	2
2	200	2	10	+1	-1	-1	6
3	100	4	10	-1	+1	-1	4
4	200	4	10	+1	+1	-1	8
5	100	2	30	-1	-1	+1	10
6	200	2	30	+1	-1	+1	18
7	100	4	30	-1	+1	+1	8
8	200	4	30	+1	+1	+1	12

Перепишем Таблицу 2.3, введя  в неё столбец фиксированной переменной . 

Таблица 2.4

№					, %
1	+1	-1	-1	-1	2
2	+1	+1	-1	-1	6
3	+1	-1	+1	-1	4
4	+1	+1	+1	-1	8
5	+1	-1	-1	+1	10
6	+1	+1	-1	+1	18
7	+1	-1	+1	+1	8
8	+1	+1	+1	+1	12

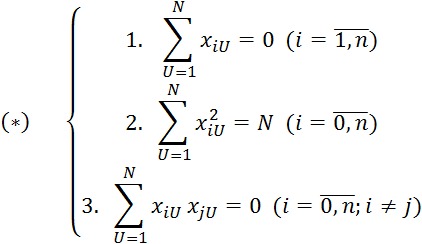
где уравнение 3. Представляет собой сумму скалярных произведений двух любых векторов-столбцов матрицы ПФЭ равных 0. Данное свойство называется свойством ортогональности.

По плану ПФЭ можно получить следующие уравнения регрессии:

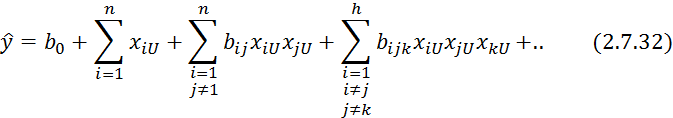
В данном уравнении максимальный эффект взаимодействия равен числу переменных.

Коэффициенты уравнения 2.7.32 определяются по методу наименьших квадратов:

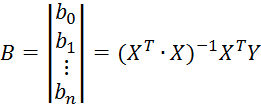
 (см. формулу 2.7.16) с учетом свойств  примет вид:

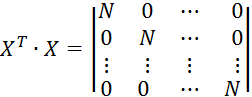
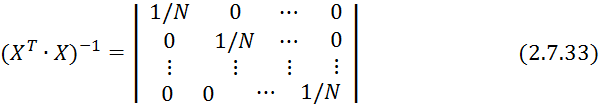
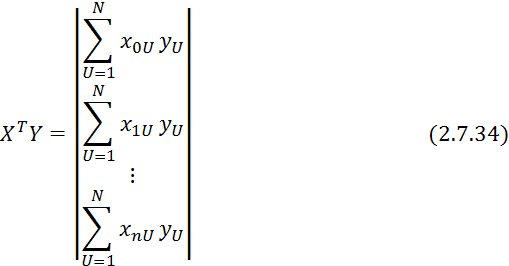
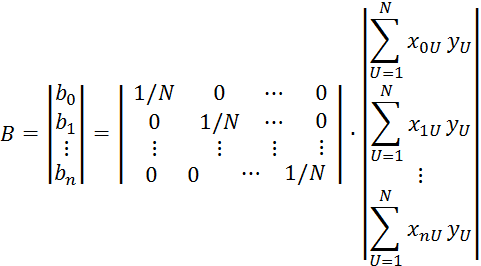
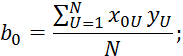
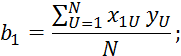
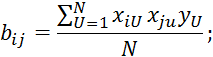
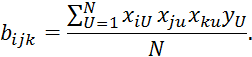
Пример:

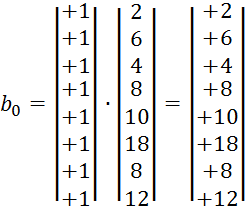
Вычисленный алгоритм методом ПФЭ содержит три обязательных проверки:

1)  На воспроизводительность опытов эксперимента;

2)  На значимость коэффициентов ,,  ;

3)  На адекватность уравнения вида 2.7.32 на экстремальных данных. 

1.   Каждый опыт повторяется -раз ; по результатам  опытов вычисляется среднее значение :

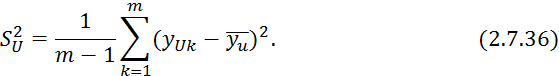
Составляется следующие соотношение:

где   — максимальная дисперсия, рассчитанная по формуле 2.7.36.

где   — табличное значение критерия Кохрена, которое выбирается из таблиц распределения Кохрена   и  — числа степеней свободы  и .

Если 2.7.38 выполняется, то ПФЭ считается воспроизводимым и его данные считаются достоверными. Причина невоспроводимости может быть малое число опытов . Если ПФЭ воспроизводим, то можно определить дисперсию вопроизводимости:

2.  Проверка на значимость ,,