Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 24

Самовыравнивание определяет устойчивость АСР и определяет способность объекта переходить к устойчивому состоянию при изменении входной величины. Основной характеристикой является степень самовыравнивания:

где  — регулирующее воздействие;

 — возмущающее воздействие;

 — установившееся значение регулируемой величины.

Ёмкость объекта характеризует его инерционные свойства, то есть его способность сохранять энергию.   

В зависимости от количества ёмкостей различают одно-, двух- и многоёмкостные объекты.

Запаздывание выражается в том, что регулируемая величина изменяется не сразу после изменения входной величины, а через некоторое время :

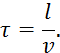
где  — расстояние от места нанесения входного воздействия до места измерения входной величины;

 — скорость измерения входной величины.

По способности восстанавливать значение регулируемой величины после изменения входной объекты делятся на:

1)  нейтральные;

2)  устойчивые;

3)  неустойчивые.

7.2.  Регулирование уровня в резервуарах

A)   Жидкость подается в резервуар самотеком через клапан, а выходит из резервуара откачиванием насосом постоянной производительности.

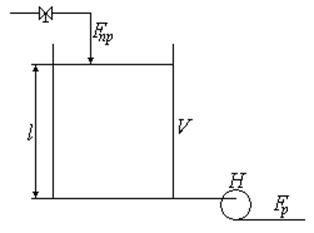
Рис. 38

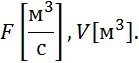
где  — притока;

 — расхода.

 — площадь сечения резервуара, ;

 — уровень.

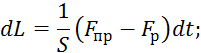
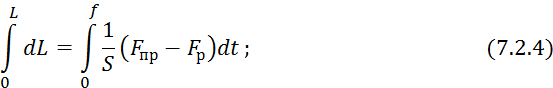
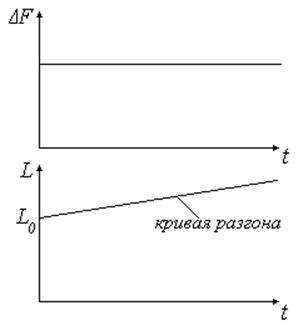
Рис. 39

Для расчета АСР математическая модель объекта необходимо представить в безразмерной форме:

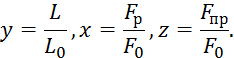
Подставим в 7.2.3 введенные обозначения:

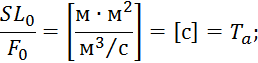
Принимаем :

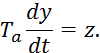
Если  то

 можно принять равным 0, так как уравнение 7.2.3 можно записать в приращениях , .

 — время разгона объекта (то время, за которое относительное изменение регулируемой величины станет равным относительному изменению возмущающего воздействия).

Данные объекты называются нейтральными.

Преобразуем по Лапласу при нулевых начальных условиях по времени уравнение 7.2.9:  при  будет равно 0.

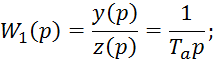
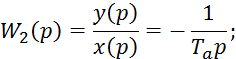
B)   Жидкость подается в резервуар самотеком и отводится из резервуара самотеком по трубопроводу с клапаном.

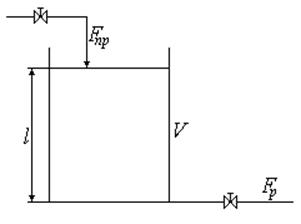
Рис. 40

Величина расхода жидкости определяется как величиной уровня, так и проходным сечением.

 — коэффициент пропорциональности клапана;

 — площадь проходного сечения.

7.2.11 можно линеаризовать, разложив в ряд Тейлора:

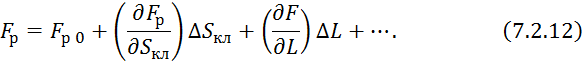
где

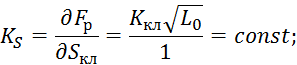
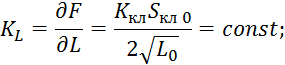
Составим уравнение материального баланса следующего вида:

Уравнение 7.2.15 подставим в 7.2.13:

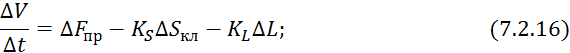
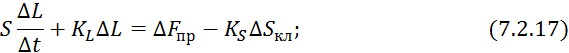
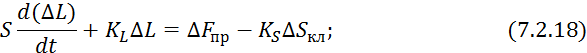
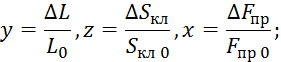
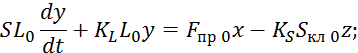
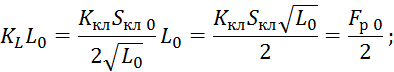
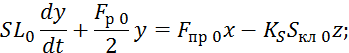
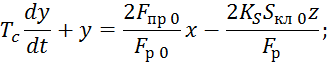
Начальные условия для 7.2.9  нулевые.

Преобразуем по Лапласу по времени 7.2.19:

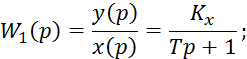
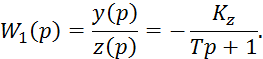
7.3.  Регулирование расхода жидких сред

Объект регулирования участок трубопровода  г:

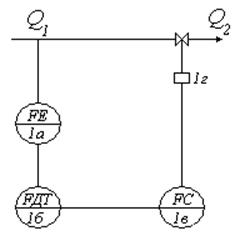
Рис. 41

где  — коэффициент пропорциональности клапана;

 — перемещение клапана.

Так как жидкость полностью заполняет сечение трубопровода, то изменение  на ту же величину изменяет , то есть .

Запишем 7.3.1 в безразмерной форме:

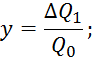
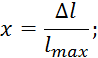
где  

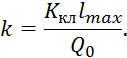
Выражение 7.3.3 преобразуем по Лапласу при :

7.4.  Регулирование расхода сыпучего материала

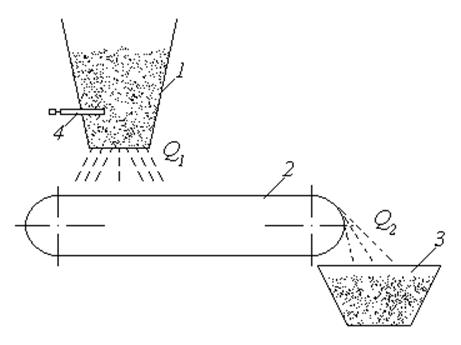
Рис. 42

4 — шибер (заслонка).

Лента конвейера перемещается со скоростью .

При равномерной загрузке ленты транспортера  определяется как:

где  — объем материала;

 — рабочая длина от места сброса из бункера 1 в место сброса в бункер 3.

В момент времени  мы увеличиваем степень открытия шибера, при этом получим:

В начальный период .

Для отрезка времени : .

Для отрезка времени : .

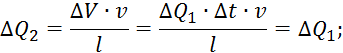
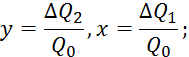
7.5.  Регулирование концентрации вещества в смесителях. Регулирование концентрации вещества в смесителях

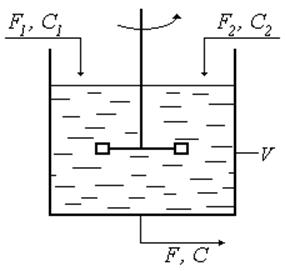
Рис. 43

 — объемные скорости потоков;

 — концентрации вещества.

 — объём смесителя.

Предполагается, что .

Переменными величинами являются .

Для нахождения уравнения динамики объекта составим уравнение материального баланса по концентрациям веществ за время :

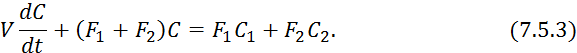
Данное уравнение является не линейным дифференциальным уравнением, поэтому приведем это уравнение, к линейному виду заменив все переменные величины суммой их значений в стационарном режиме к приращением:

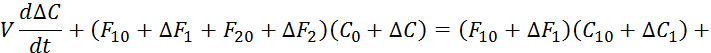
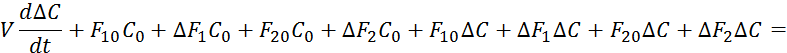
Запишем уравнение 7.5.3 для стационарного режима:

Вычтем из 7.5.5 уравнение 7.5.6:

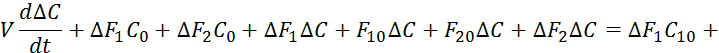
Так как приращение переменных малы, то и их произведения мало, то есть приблизительно равно нулю.