Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 19

1)  Режим движения теплоносителя — идеальное вытеснение;

2)  Величина теплообмена между первичным и вторичным теплоносителем описывается:

где  — коэффициент теплопередачи.

3)  Теплоемкость стенки мала по сравнению с теплоемкостью частиц теплоносителя, поэтому можно не учитывать накопление тепла в стенке;

4)  При изменении -ры одного из теплоносителей теплообмен происходит мгновенно.

4.1.  Прямоточные кожухотрубчатые теплообменники

Пусть имеется теплообменник (Рис. 30):  

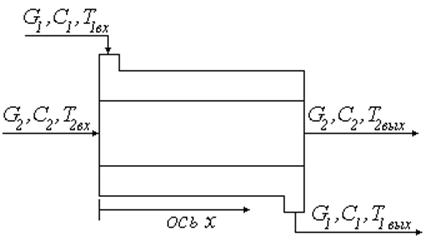
Рис. 30

где , — весовые расходы;

, — теплоемкости.

Выделим участок  (Рис. 31):

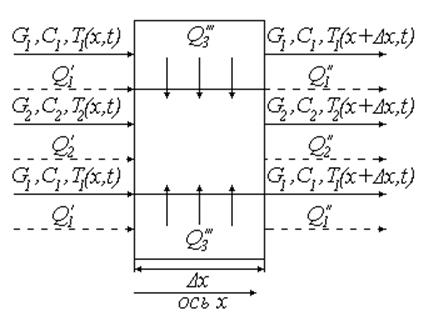
Рис. 31

где  — количество теплоты, поступающее в участок с первичным теплоносителем за время ;

 — количество теплоты переходящее на участке  от первичного к вторичному теплоносителю за время :

Изменение энтальпии на участке  за время :

где  — площадь сечения первичного потока;

 — плотность частиц потока.

Разделим левую и правую часть на  и возьмем предел:

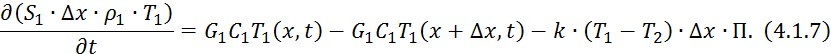
Разделим на :

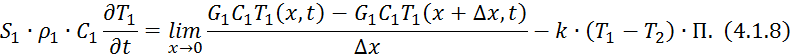
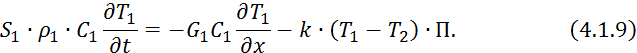
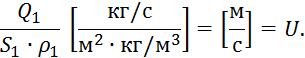
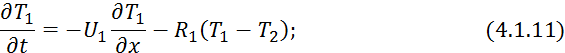
где

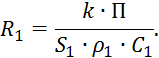
Уравнение 4.1.11 является уравнением профиля температур первичного теплоносителя.

Аналогично можно получить уравнение профиля температур вторичного теплоносителя:

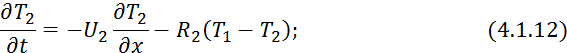
где

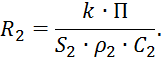
4.2.  Противоточный кожухотрубчатый теплообменник

Пусть имеется теплообменник (Рис. 32):  

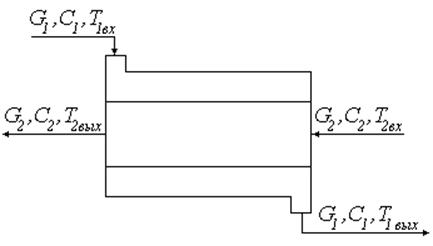
Рис. 32

Выделим участок  (Рис. 33):

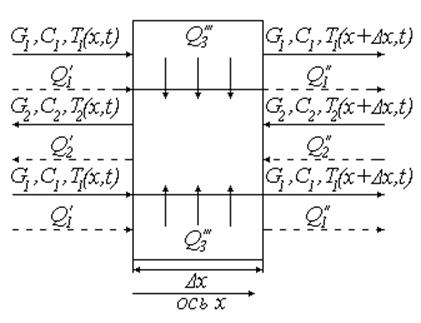
Рис. 33

Для данного теплообменника уравнение профиля температур аналогично уравнению для прямоточного теплообменника:

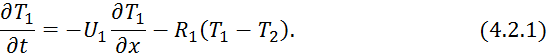
Так как направление вторичного теплоносителя противоположно направлению первичного, то в уравнении 4.1.12 изменится знак при :

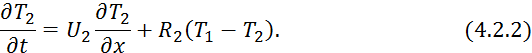
Приведение уравнения профиля температур для прямоточного 4.1.11 и 4.1.12 и противоточного 4.2.1 и 4.2.2 не учитывают накопление тепла в стенке разделяющих теплоносители. Это справедливо при:

1)  Теплоёмкость стенки намного меньше  и ;

2)  Коэффициент передачи  должно быть большим. Это условие обеспечивается, если оба теплоносителя в жидком виде.

Если один из теплоносителей газ (пар), то  значительно уменьшается и необходимо при математическом моделировании учитывать накопление тепла в стенке.

4.3.  Математические модели теплообменников с учетом накопления тепла в стенке

 — температура стенки;

,  — температуры первичного и вторичного теплоносителей.

Удельное количество тепла, передающееся от теплоносителя к станке выражается:

Удельный тепловой поток от стенки ко второму теплоносителю выражается:

4.3.1.  Прямоточный кожухотрубчатый теплообменник

Выделим участок :

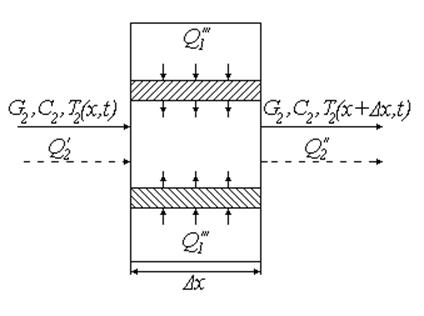
Рис. 33

Для данного теплообменника  рассчитывается по формуле 4.1.3.  — количество теплоты, передающееся от первичного теплообменника к стенке:

С учетом 4.3.3 уравнение профиля температур первичного теплоносителя примет вид:

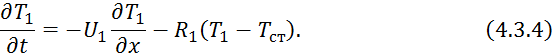
где 

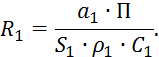
Для количества теплоты ,  эти величины соответствуют тем же значениям, что и для прямоточного теплообменника.

 — количество тепла, передающееся к вторичному теплоносителю.

С учетом 4.3.5 уравнение профиля температур для вторичного теплоносителя примет вид:

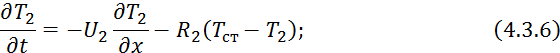
где 

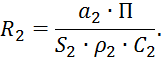
Система уравнений 4.3.4 и  4.3.6 является незамкнутой, так как в ней отсутствует уравнение для изменения температуры станки. Для этой цели определим уравнение изменения энтальпии участка стенки  за время .

Подставим 4.3.3 и 4.3.5 в 4.3.7, получим:

Разделим на  и возьмем предел при :

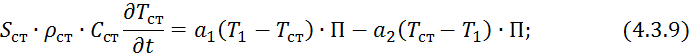
Разделим левую и правую часть на :

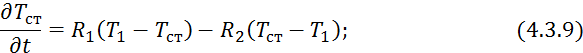
где 

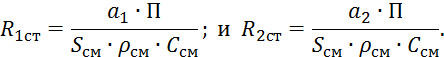
4.3.2.  Противоточный кожухотрубчатый теплообменник

Направление оси  принимаем по направлению первичного потока, а направление вторичного потока противоположно.

При математическом моделировании данного теплообменника уравнения 4.3.4 и 4.3.10 будут те же, а в уравнении 4.3.6 изменятся знаки при : 

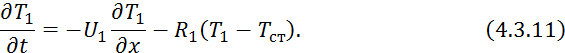
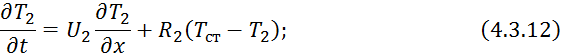
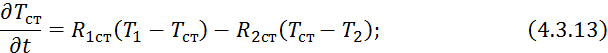
4.4.  Математическая модель конденсатора (паровой теплообменник)

В этом теплообменнике пар, поступающий в него, полностью конденсируется. Температура пара определяется давлением в данном теплообменнике. Так как давление в замкнутом теплообменнике постоянно, то это означает. Что температура пара постоянная, то есть температура не изменяется по линейной координате (=0, ).