Эмпирическая
зависимость между величинами ![]() и
и ![]() получена только для стационарного режима работы.
Для нестационарного режима:
получена только для стационарного режима работы.
Для нестационарного режима:
![]()
Аналогично можно получить уравнение математического баланса для газа:
![]()
![]()
![]()
Подставим 5.1.12 и 5.1.13 в 5.1.2:
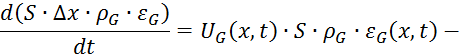
![]()
Разделим 5.1.14 на ![]() и перейдя в
правой части к пределу получим:
и перейдя в
правой части к пределу получим:

Получим
уравнение профиля поглощаемого компонента ![]() в газовой фазе.
в газовой фазе.
Запишем уравнение материального баланса для данного компонент:
![]()
![]()
![]()
![]()
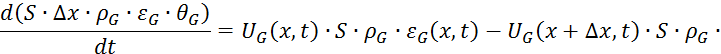
![]()
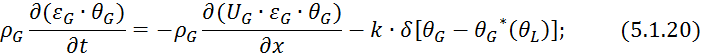
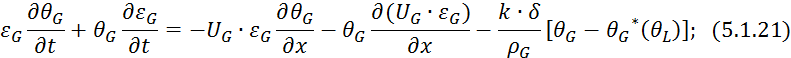
Умножим 5.1.15 на величину ![]() :
:
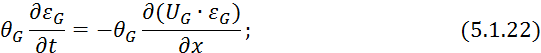
Вычтем из уравнения 5.1.22 уравнение 5.1.21:
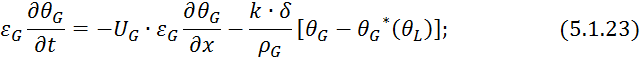
Разделим
5.1.23 на ![]() :
:
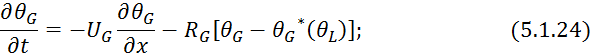
где
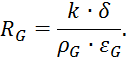
5.1.24
—
уравнение профиля концентрации поглощаемого компонента в газовом потоке на слое
осадок толщиной ![]() .
.
Аналогично можно получить уравнение профиля поглощаемого компонента в жидкости.
Данное уравнение будет иметь вид:
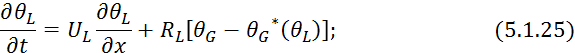
В данном
уравнении по сравнению с 5.1.24 изменен знак при ![]() и
и ![]() (т.к. концентрация поглощаемого компонента
увеличивается за счет поглощения жидкого компонента).
(т.к. концентрация поглощаемого компонента
увеличивается за счет поглощения жидкого компонента).
Таким образом,
при переменных весовых расходах ![]() ,
, ![]() математическая модель газоабсорбера включает:
математическая модель газоабсорбера включает:
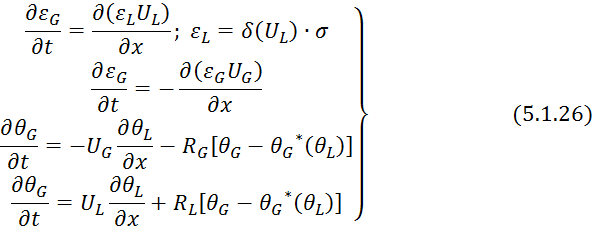
Если
![]() и
и ![]() , то
, то
![]() и
и ![]() ;
;
и математическая модель газоабсорбера примет вид:
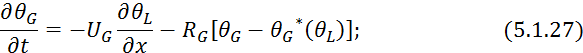
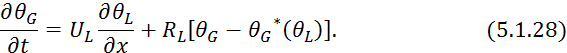
Зависимость ![]() является нелинейной, поэтому система уравнений
5.1.27 и 5.128 является не линейной. Задачей является линеаризовать данную
систему:
является нелинейной, поэтому система уравнений
5.1.27 и 5.128 является не линейной. Задачей является линеаризовать данную
систему:
![]()
где Г — константа Генри.
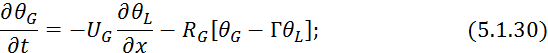
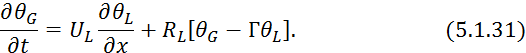
Обозначим
![]() и умножим 5.1.31 на Г:
и умножим 5.1.31 на Г:
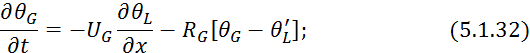
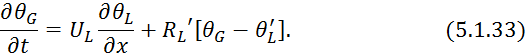
по структуре данная система уравнений аналогична системе уравнений кожухотрубчатого противоточного теплообменника 4.5.43 и 4.5.44.
![]()
Передаточная функция газоабсорбера аналогична передаточной функции данного теплообменника.
5.2. Математическая модель процесса ректификации
Данный процесс проходит в насадочной и тарельчатой колоннах.
Математическое описание процесса ректификации в насадочных колоннах аналогично математическому описанию газоабсорберов.
Рассмотрим математическое описание бинарной смеси в тарельчатой колонне.
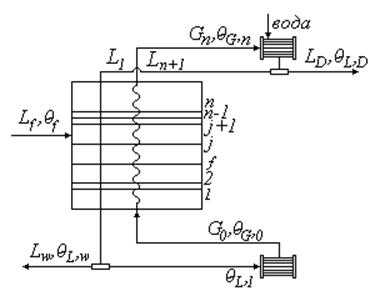
Рис. 34
где
![]() ,
, ![]() ,
, ![]() — мольные расходы питания дистиллята и кубового
остатка;
— мольные расходы питания дистиллята и кубового
остатка;
![]() — концентрация низкокипящего компонента в паровой
фазе.
— концентрация низкокипящего компонента в паровой
фазе.
![]() — концентрация низкокипящего компонента в жидкой
фазе;
— концентрация низкокипящего компонента в жидкой
фазе;
![]()
![]() — мольный расход жидкости, поступающий в
испаритель;
— мольный расход жидкости, поступающий в
испаритель;
![]() — мольная концентрация низкокипящего компонента в
жидкой фазе;
— мольная концентрация низкокипящего компонента в
жидкой фазе;
![]() — мольный расход пара;
— мольный расход пара;
![]() — концентрация;
— концентрация;
Математическая модель процесса ректификации включает в себя модели тарелок, куба испарителя и дефлегматора.
Схема -ой тарелки:
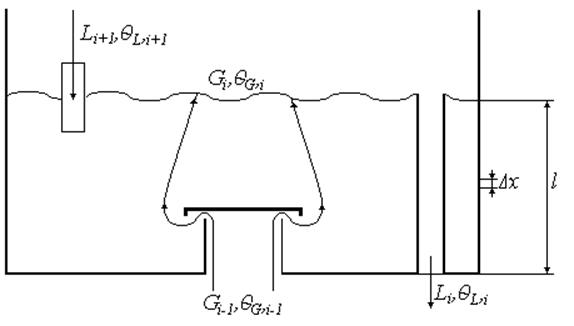
Рис. 35
где ![]() ,
, ![]() — мольный поток жидкости и газа на входе в -тую
тарелку;
— мольный поток жидкости и газа на входе в -тую
тарелку;
![]() ,
,![]() — мольная концентрация низкокипящего компонента в
жидкости и в паре на ходе;
— мольная концентрация низкокипящего компонента в
жидкости и в паре на ходе;
![]() ,
, ![]() — мольный поток жидкости и пара на выходе из -той
тарелки;
— мольный поток жидкости и пара на выходе из -той
тарелки;
![]() ,
,![]() — мольная концентрация низкокипящего компонента в
жидкости и в паре на выходе из -той тарелки.
— мольная концентрация низкокипящего компонента в
жидкости и в паре на выходе из -той тарелки.
Принимается
течение жидкости на ![]() -той тарелке
происходит в режиме идеального перемешивания, для газа — идеального
вытеснения.
-той тарелке
происходит в режиме идеального перемешивания, для газа — идеального
вытеснения.
Так как мольные теплоты парообразования всех жидкостей одинаков, то есть количество молей низкокипящего компонента перешедшего из жидкости в пар и количество молей высококипящего компонента примерно одинаково.
Массообмен на![]() -той тарелке
определяется в виде:
-той тарелке
определяется в виде:
![]()
где
![]() — удельный мольный момент расход или поток
низкокипящего компонента переходящего из жидкости в пар.
— удельный мольный момент расход или поток
низкокипящего компонента переходящего из жидкости в пар.
Для вывода математической модели тарелки используется уравнение материального баланса:

Запишем 5.2.2 для мольного потока жидкости на -той тарелке:
![]()
где
![]() — количество жидкости на тарелке;
— количество жидкости на тарелке;
![]() — количество жидкости поступающей на тарелку.
— количество жидкости поступающей на тарелку.
![]()
где
![]() — количество жидкости уходящей из тарелки.
— количество жидкости уходящей из тарелки.

Аналогично находится уравнение для пара:

Так как пар или
газ довольно быстро проходит через слой жидкости, то накопление его на тарелке
не происходит, то есть ![]() , то
, то
![]()
Получим
уравнение профиля концентрации низкокипящего компонента в жидкости на -той
тарелке ![]() :
:
![]()
![]()
![]()
где ![]() — количество низкокипящего компонента перешедшего
из жидкости в газ в единицу времени.
— количество низкокипящего компонента перешедшего
из жидкости в газ в единицу времени.
Для нахождения ![]() выделим на тарелке слой толщиной
выделим на тарелке слой толщиной ![]() :
:
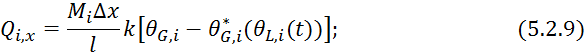
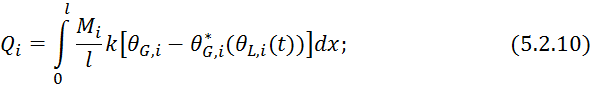
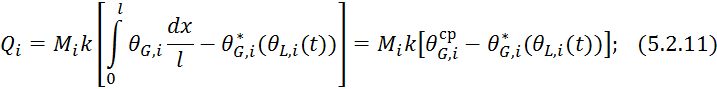
![]()
Подставляем 5.2.6 и 5.2.7 в 5.2.12:
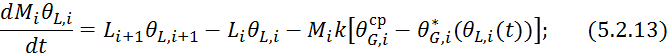
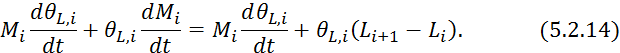
Подставим левую часть в 5.1.12:
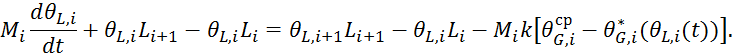
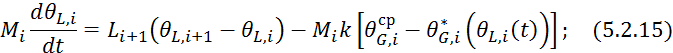
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.