Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 25

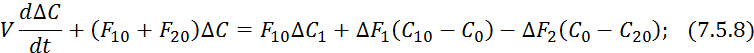
Выражение 7.5.8 представим в безразмерных величинах:

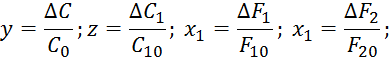
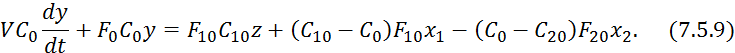
Разделим на коэффициент при :

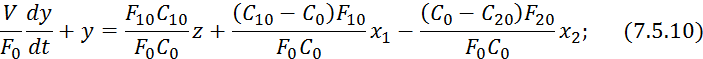
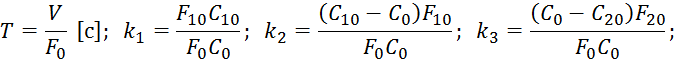
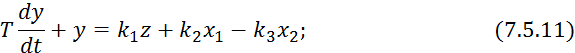
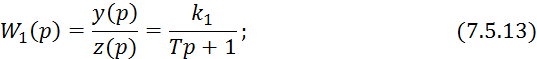
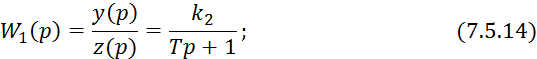
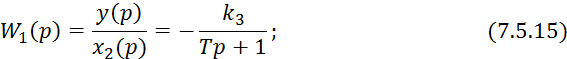
7.6.  Регулирование температуры в смесителях идеального перемешивания

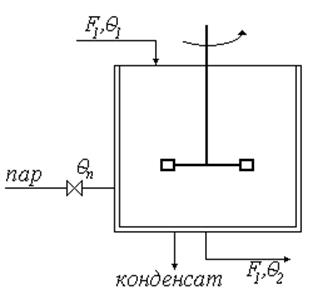
Рис. 44

где  — линейная скорость;

 — температура.

.

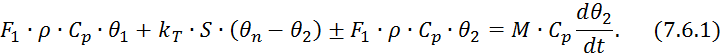
где  — плотность жидкости;

 — удельная теплоемкость жидкости;

 — коэффициент теплоотдачи от пара;

 — вес жидкости в смеси;

 — тепловой поток, поступающий в смеситель с жидкостью:

 — тепловой поток за счет теплообмена между паром и жидкостью;

 — тепловой поток, уходящий из смесителя;

 — накопление тепла.

Представим переменные величины как сумму в стационарном режиме и приращения:

Для нестационарного режима работы:

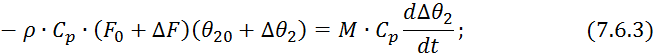
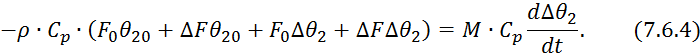
Приращение малы, следовательно, произведения приращений малы, то есть приблизительно равны нулю.

Вычтем из уравнения 7.6.4 уравнение 7.6.2:

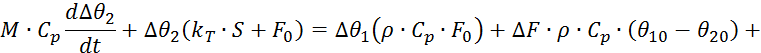
Разделим все члены выражения 7.6.6 на коэффициент при :

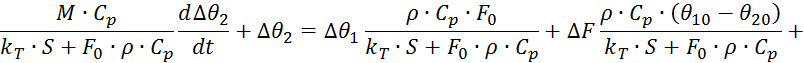
где

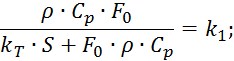
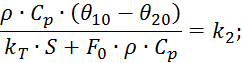
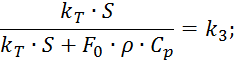
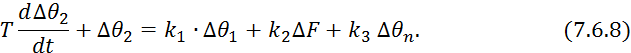
Начальные условия:

Преобразуем по Лапласу уравнение 7.6.8:

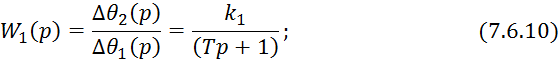
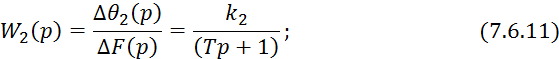
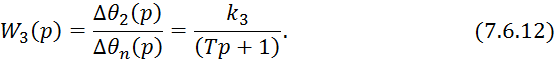
7.7.  Регулирование состава смеси в реакторе с мешалкой

Скоростью химической реакции в данном реакторе можно управлять, изменяя состав подаваемых компонентов и потоки. Для регулирования состава необходимо поддерживать постоянство состояния потоков материалов, подводимых к реактору.

Возмущение по составу в потоке вызывает изменение состава среды в реакторе.

Схема регулирования состава в реакторе.

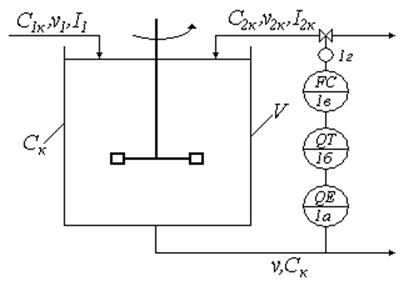
Рис. 45

где  — объемная скорость [м/с];

 — величина потока ;

 — концентрация .

В реакторе протекает реакция первого порядка:

Задача обеспечить заданную величину .

Поток  — возмущающее воздействие;

 — регулирующее воздействие.

Составим уравнение динамики объекта в виде следующего уравнения материального баланса:

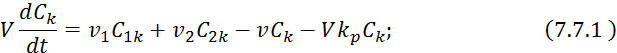
где  — изменение концентрации;

 — величина потока выходящего из реактора;

 — величина потока поступающего в реактор;

 — изменение концентрации за счет химической реакции.

Пример  и  постоянны, .

Переменные величины представляем в виде суммы значений стационарного режима и приращения:

  

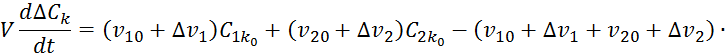
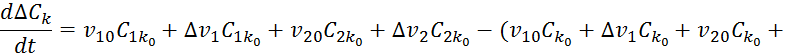
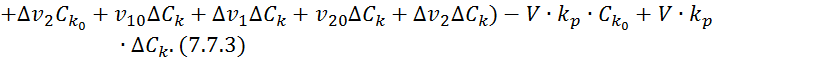
Составим уравнение 7.7.1 для стационарного режима работы реактора:

Принимаем небольшие приращения переменных, следовательно, их произведения приблизительно равны нулю.

Вычитаем из уравнения 7.7.3 уравнение 7.7.4:

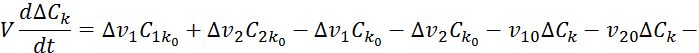
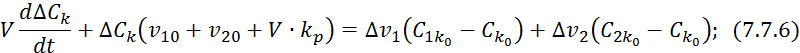
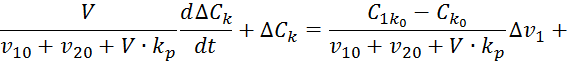
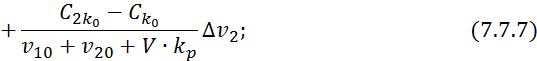
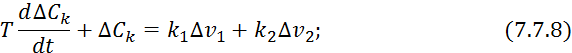
Также можно получить передаточные функции объекта при переменных величинах , , и т.д..

8.  Методы и алгоритмы идентификации динамических систем

Под идентификацией понимается получение и уточнение по экспериментальным данным модели объекта (процесса) выраженной в тех или иных терминах, то есть описанной на том или ином языке.

Получение или уточнение по экспериментальным данным модели объекта работоспособной для всех режимов называется идентификацией объекта. При исследовании одного режима работы объекта называют идентификации работы.

8.1.  Общая классификация задач идентификации

Классификация осуществляется по ряду следующих признаков:

1)  Идентифицируемый объект (процесс);

2)  Класс моделей в терминах, которых осуществляется идентификация;

3)  Условия наблюдения, виды возбуждающих воздействий.

В практике идентификации сам объект оказывает определяющее воздействие на условия наблюдения и определяет условия возбуждения и др..

В теории идентификации применяются две модели:

1)  Модель, описывающая идентифицированный объект;

2)  Модель, в терминах которой осуществляется идентификация.

Эти модели по своей форме могут совпадать или не совпадать. Последнее имеет место в том случае, если идентифицируемый объект в интересах простоты идентификации, описывается более простой моделью, чем модель идентифицируемого объекта.

Эффективность идентификации проверяется путем сравнения реакции реального объекта и модели полученной в результате идентификации на реальное возбуждение.

8.2.  Постановка задачи идентификации

Понятие функциональных метрических пространств (частный случай множеств) настолько широкое, что любые входные и выходные сигналы реального объекта можно рассматривать как часть пространств.