Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 22

Получим уравнение профиля концентраций низкокипящего компонента в паровой фазе на -той тарелке:

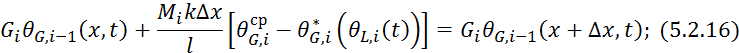
где  — входной поток;

 — массообмен;

 — выходной поток.

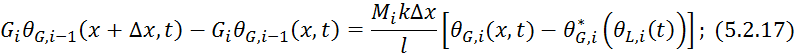
Разделим левую и правую часть на  и найдем предел при  :

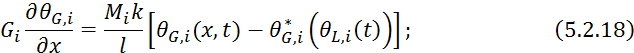
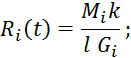
Уравнение 5.2.15 можно упростить следующим образом:

проинтегрируем выражение 5.2.18 от 0 до  по  и получим выражение:

Подставим левую часть 5.2.22 в 5.2.15:

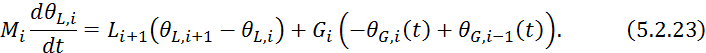
5.2.23 уравнение профиля концентраций низкокипящего компонента в жидкости.

5.2.21 уравнение профиля концентраций низкокипящего компонента в паровой фазе.

Данные уравнения справедливы для любой тарелки, кроме питающей:

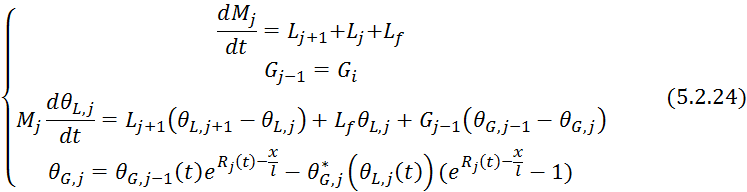
5.2.24 математическая модель для -той тарелки.

При выводе моделей куба испарителя и дефлегматора принимается следующие допущение:

Тепло- и массообменные процессы довольно сложны, поэтому можно ограничиться уравнениями статики для этих процессов. Это справедливо, так как данные процессы проходят быстрее, чаем на тарелке.

Для куба испарителя:

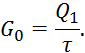
где  — количество теплоты поступающей в куб испаритель;

 — мольная теплота испарения бинарной смеси.

Для дефлегматора:

5.3.  Передаточная функция ректификационной колонны

Передаточная функция -той тарелки:

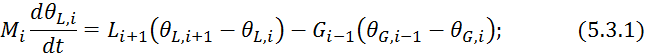
где входные величины:

 — расход жидкости;

 — расход паре;

, .   

Выходные величины:

, .   

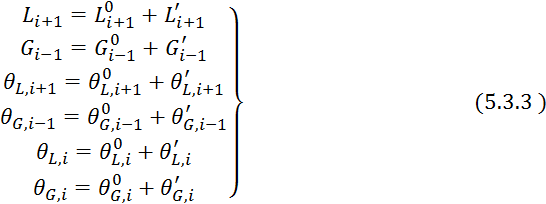
С индексом “ ⁰ ” — стационарные значения, с индексом “ ’ ” — приращение параметра в переходном режиме.

Запишем 5.3.1 для стационарного режима:

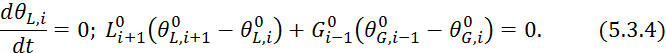
Запишем 5.3.2 для стационарного режима:

Получим передаточную функцию по следующему каналу  в этом режиме все остальные переменные принимаются в стационарном режиме, кроме данного входа:

   ,  .

Решаем 5.3.1 для данных условий:

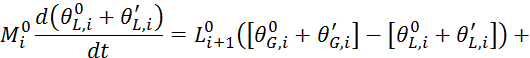
Запишем 5.3.2 для данных условий:

Вычитаем из 5.3.7 уравнение 5.3.4:

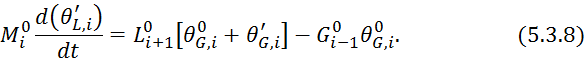
Вычитаем из 5.3.7 уравнение 5.3.5:

где

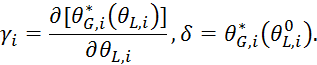
Перепишем 5.3.10 в виде:

С учетом 5.3.12 упростим 5.3.9:

Подставим 5.3.13 в 5.3.8:

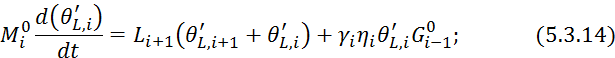
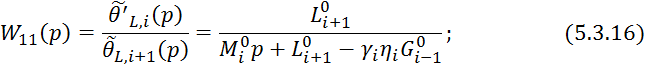
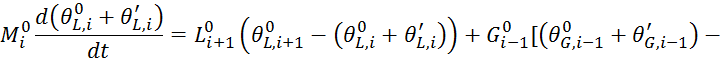
Вычитаем из 5.3.17 уравнение 5.3.5:

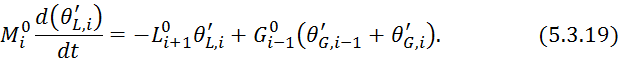
Вычитаем из 5.3.18 уравнение 5.3.5:

Подставляем 5.3.20 в 5.3.19:

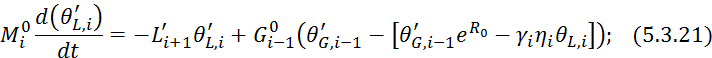
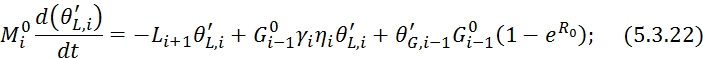
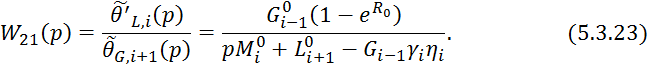
Канал

,  — стационарные значения.

Запишем 5.3.1  стационарных условий:

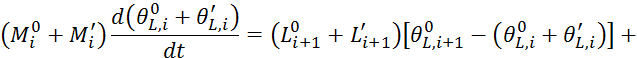
Запишем уравнение 5.3.2:

Вычтем из 5.3.24 уравнение 5.3.4:

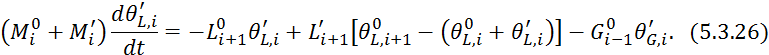
Преобразуем 5.3.26:

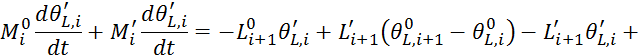
Так как приращения переменных принимаем равными небольшим переменным,  следовательно, произведение небольших приращений приблизительно равно нолю.

Начальными условиями для 5.3.28 будут:

Преобразуем по Лапласу по времени уравнение 5.3.26:

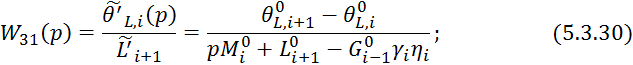
Канал

,  — стационарные значения.

Запишем 5.3.1  стационарных условий:

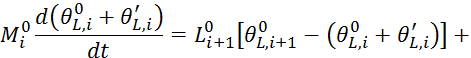
Запишем уравнение 5.3.1 для данных условий:

Вычтем из 5.3.32 уравнение 5.3.4:

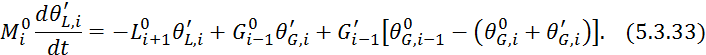
Вычтем из 5.3.32 уравнение 5.3.5:

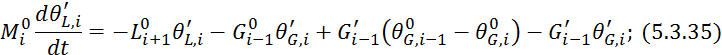
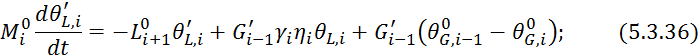
Преобразуем по Лапласу по времени 5.3.36:

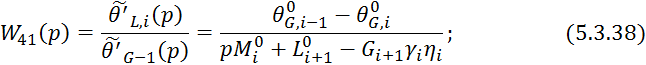
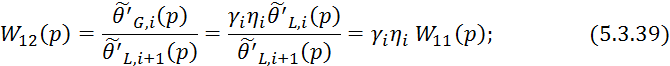
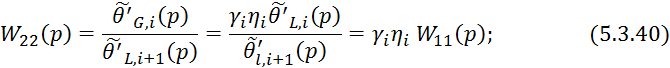
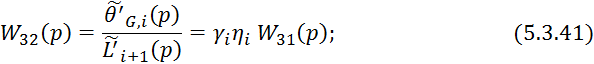
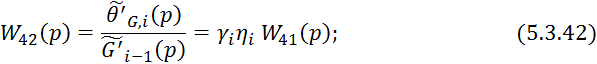
Процессы тепло- и массопередачи проходящие в кубе-испарителе  и дефлегматоре протекают намного быстрее чем на тарелке, поэтому передаточная функция по каналам этих частей можно представить в виде усилительных звеньев для получения которых можно использовать вышеприведенные статические зависимости.

6.  Математическое моделирование математических процессов

6.1.  Математическая модель процесса химического превращения (кинетическая модель)

Протекание химической реакции можно описать следующим стехиометрическим уравнение:

 — исходные компоненты реакции;

 — продукты реакции;

 — стехиометрические коэффициенты;

 — стехиометрические коэффициенты.

Уравнение 6.1.1 можно представить в более общем виде:

Пусть в реакторе протекает -реакций:

в реакции участвуют  веществ.

Уравнение 6.1.1 примет вид:

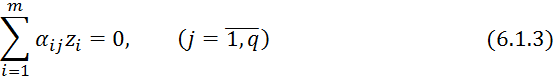
где   — стехиометрический коэффициент -той реакции по -тому компоненту.

 — для исходных компонентов;

 — для продуктов реакции.

Если  -тое вещество не участвует в -той реакции, то .

Основной характеристикой химической реакции является её скорость. Скорость. Химической реакции по -тому компоненту называется изменение компонента в единицу времени:

Зная скорость химической реакции по одному из компонентов можно определить скорость по остальным:

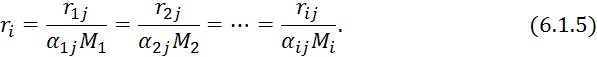
где   — количество молей -того вещества участвующего в -той реакции;