Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 15

№
1	+1	-1	-1	+1	1/3	1/3
2	+1	+1	-1	-1	1/3	1/3
3	+1	-1	+1	-1	1/3	1/3
4	+1	+1	+1	+1	1/3	1/3
5	+1	+1	0	0	1/3	-2/3
6	+1	-1	0	0	1/3	-2/3
7	+1	0	+1	0	-2/3	1/3
8	+1	0	-1	0	-2/3	1/3
9	+1	0	0	0	-2/3	-2/3

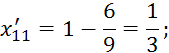
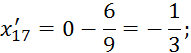
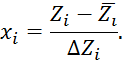
По данным Таблицы 2.10 можно получить следующие уравнения регрессии:

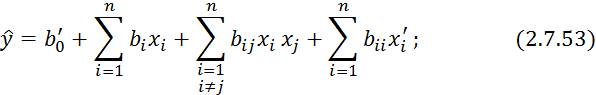
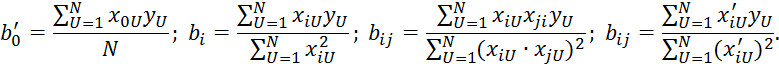
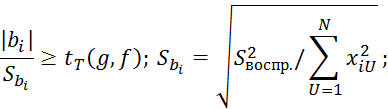
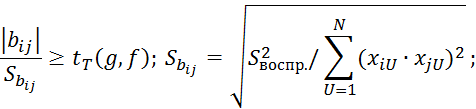
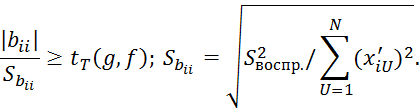
В ортогональных планах второго порядка коэффициенты регрессии вида 2.7.53 оцениваются с различной точностью.

Запишем уравнение 2.7.52 для :

Вычислительный алгоритм для ортогональных планов второго порядка включает те же планы, что и для первого порядка. Отличие заключается в оценке значимости коэффициентов уравнения 2.7.53 с учетом различных значений величин , ,  .  

Д)   Симплекс планирования экспериментов и оптимизация химико-технологических процессов.

Необходимо получить материальную модель некоторого химико-технологического (ХТП) в виде уравнения регрессии:

Для этой цели имеется симплекс метод.

Под правильным симплексом понимается совокупность  равноудаленных точек в -мерном факторном пространстве, то есть исходная серия представляет правильный симплекс. Каждая точка в пространстве — это условие.

Количество опытов

В каждой точке измеряется значение  при определённом значении .

По результатам исходной серии опытов определяется точка отбрасывания и при планировании  опыта определяются координаты зеркального отображения (по всем осям ) данной наихудшей точки относительно центра. Мы получаем новый симплекс, который включает все остальные точки кроме наихудшей. И опять оцениваем величины  в новом и находим наихудшую точку, производим её зеркальное отображение, и т.д.. то есть происходит процесс передвижения в область наибольших значений .

 отрезок,

 равносторонний треугольник,

 тетраэдр.

Пример: .

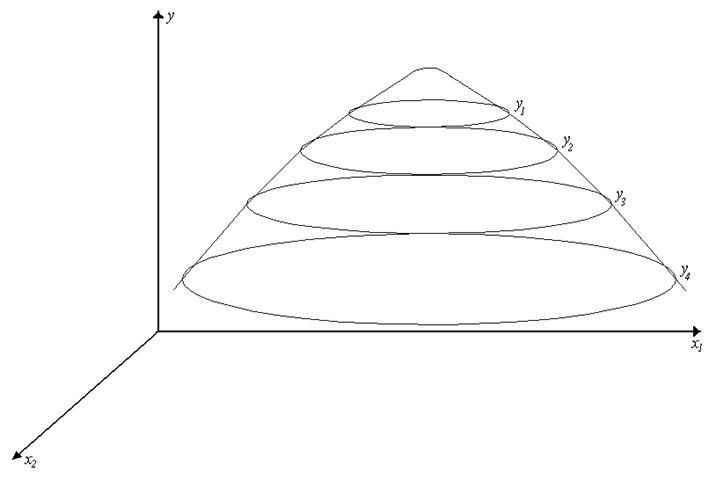
Рис. 15

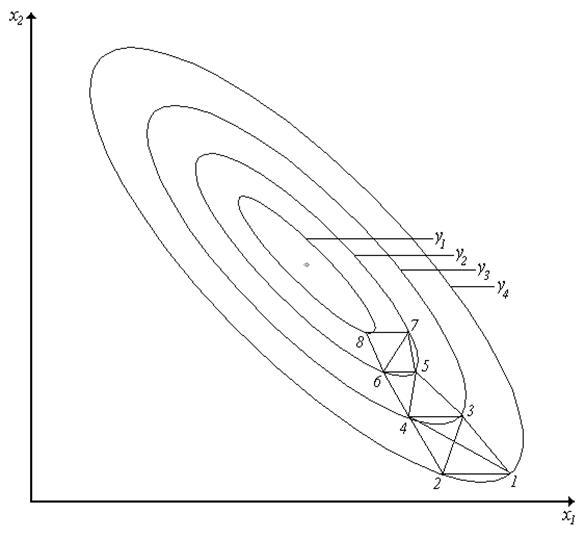
Рис. 16

Рисуем произвольно треугольник, определяем наихудшую точку относительно . Наихудшая точка 1, 2, 3. Отображаем зеркально точу 1 и получаем 4, следовательно, получаем новый симплекс.    

В результате продвижения мы попадаем в почти стационарную область, то есть область близкую к .

Можно доказать, что если экспериментальные точки в факторном пространстве соответствуют следующей матрице:

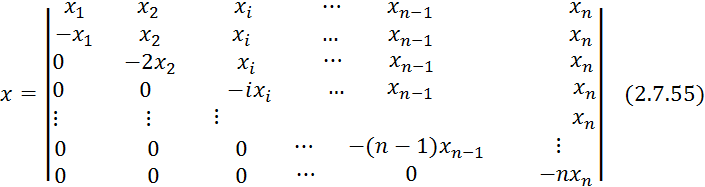
То данные экспериментальные точки образуют правильный симплекс с центром в начале координат  и опорной равной 1.

Рассмотрим свойства матрицы данного плана:

1)   

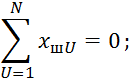
2)   

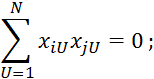
3)   

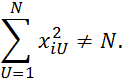
Количество строк :

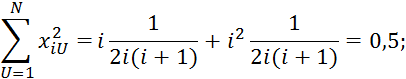
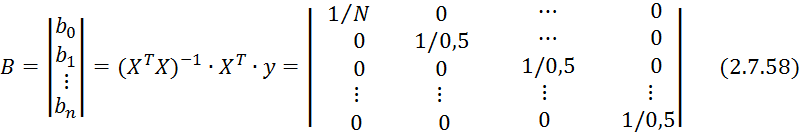
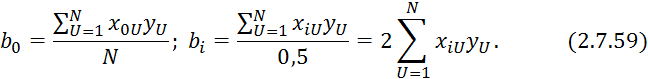
Так как количество коэффициентов  в уравнении 2.7.57 рано количеству опытов в симплекс-планировании, то такой план называется насыщенными

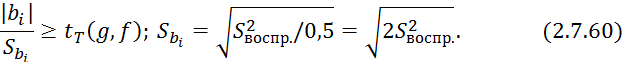
 в симплекс-планировании намного выше чем в ортогональном планировании первого прядка, то есть коэффициенты в уравнении регрессии в  симплекс-планировании оценивается с большой погрешнотью.

Для реализации плана 2.7.55 необходимо элементы матрицы представить в численном виде с помощью 2.7.56:

 

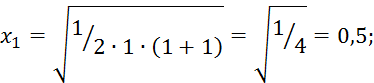
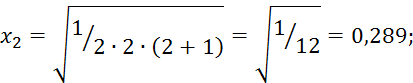
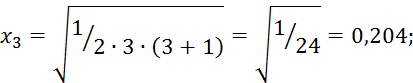
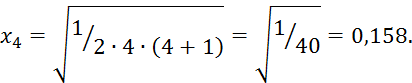
 =5

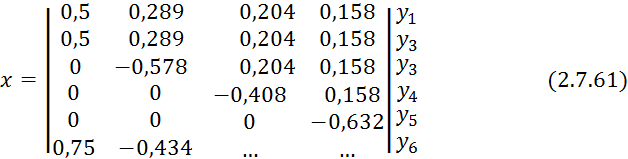
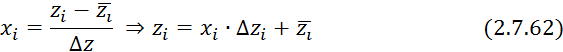
С применением формулы 2.7.61 матрицу 2.7.61 представим в размерных величинах .

Далее по результатам проведения опытов правильного симплекса определяется наихудшая точка, то есть точка с наименьшим значением , далее эта точка отбрасывается, и определяются координаты данной наихудшей точки относительно центра противоположной грани.

Координаты центра противоположной грани по -тому фактору определяются:

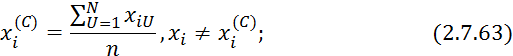
где   — координата по -тому фактору наихудшей точки.

Координаты отраженной по-тому фактору: