Любой химико-технологический процесс (ХТП) сопровождается перемещениями потоков, которые могут быть однофазными и многофазными, поэтому необходимо получить математическое описание этих потоков, то есть гидродинамику. Однако, гидродинамика многофазных потоков сложна.
При моделировании гидродинамики сложных ХТП будем прибегать к упрощенному варианту свойств многофазных потоков, сводя эти свойства к более простому варианту.
Структура потоков определяется степенью перемешивания частиц вещества данного потока, которая определяет поле концентрации.
По степени перемешивания можно выделить следующие типовые структуры потоков и соответствующие им математические описания:
— модель идеального перемешивания;
— модель идеального вытеснения;
модели, описывающие гидродинамик реальных потоков:
— диффузия модели;
— ячеечные модели;
— комбинированные модели.
Универсальным описанием данных моделей является однородные дифференциальные уравнения или дифференциальные уравнения в частных производных отражающие изменение концентрации.
Требования к моделям:
1) Должна быть обеспечена возможность расчета коэффициентов модели;
2) С помощью их необходимо исследовать гидродинамику потоков и оптимизировать гидродинамичный режим.
При моделировании гидродинамики сложных ХТП изучается основные свойства, производятся некоторые упрощения этих свойств, и эти свойства сводятся к одной из типовых структур потоков с известной моделью.
Если в аппарате несколько потоков, то для каждого из потоков разрабатывается материальное описание.
3.3. Модель идеального перемешивания
За структуру потока соответствующую модели идеального перемешивания принимают следующие:
Поток среды, поступающий в аппарат, мгновенно распределяется по всему объему аппарата и концентрация вещества в каждой точке аппарата и на его выходе одинакова.
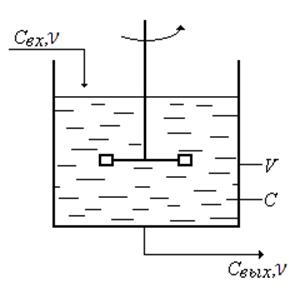
Рис. 18
где
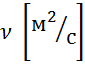 — объемная скорость;
— объемная скорость;
![]() — объем зоны идеального перемешивания;
— объем зоны идеального перемешивания;
![]()
![]()
![]()
Для
стационарного режима: ![]() ,
, ![]() ,
, ![]()
Для нестационарных режимов:
![]()
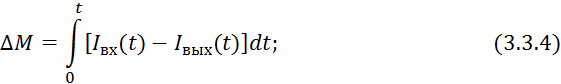
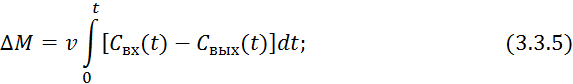
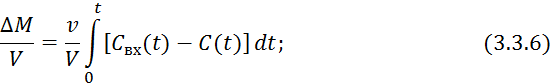
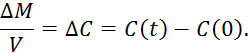
где
![]() — концентрация в установившимся режиме.
— концентрация в установившимся режиме.
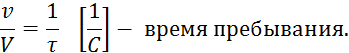
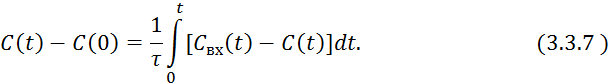
Продифференцируем 3.3.7 пот времени:


Преобразуем по Лапласу при нулевых начальных условиях выражение 3.3.9:
![]()
![]()
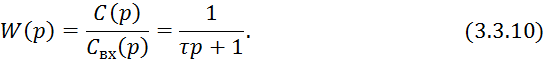
Решение уравнения 3.3.8
зависит от вида ![]() . Если:
. Если:
1) ![]() , то
, то
![]()
Выражение 3.3.11 называется F-кривой.
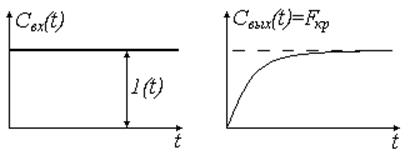
Рис. 19
2) ![]() , то
, то
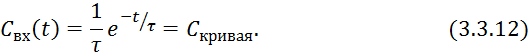
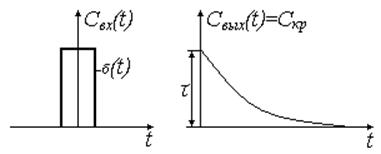
Рис. 20
Если при
исследовании неизвестной структуры потока, полученные экспериментальные ![]() и
и ![]() кривой
совпадают с расчетными, то модели можно отнести к модели идеального
перемешивания.
кривой
совпадают с расчетными, то модели можно отнести к модели идеального
перемешивания.
На практике
часто стремясь получить модель идеального перемешивания, снабжаются их
мешалками. Наиболее лучшему режиму идеального перемешивания соответствуют
ёмкостные аппараты, проточного типа снабженные мешалками при небольшой объемной
скорости и при условии 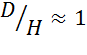 .
.
3.4. Модель идеального вытеснения
За структуру потока соответствующую модели идеального вытеснения (МИВ) принимается поршневое течение вещества без перемешивания частиц в продольном направлении, при равномерном распределении концентрации вещества в сечении перпендикулярных направлению движения потока.
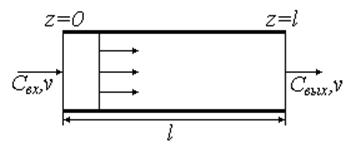
Рис. 21
![]()
где
![]() — линейная координата;
— линейная координата;
![]()
где
![]() — объемная скорость;
— объемная скорость;
![]() — линейная скорость потока;
— линейная скорость потока;
![]() — сечение потока.
— сечение потока.
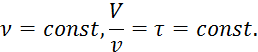
Для вывода
уравнения модели идеального вытеснения выделим -тую элементарную ячейку,
объемом ![]() , длинной
, длинной ![]() и сечением
и сечением ![]() .
.
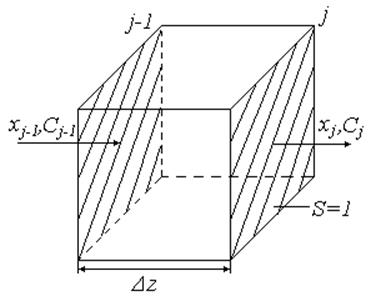
Рис. 21
![]()
![]()
Для стационарных режимов:
![]()
Для нестационарных режимов:
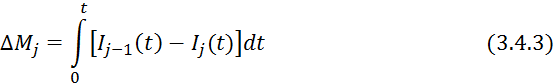
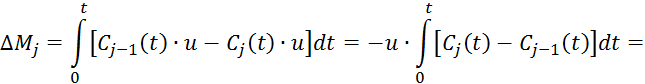

Разделим 3.4.4
на ![]() :
:
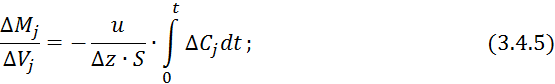
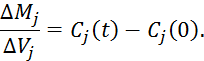
Так как ![]() не зависит от
времени, введем его под знак интеграла:
не зависит от
времени, введем его под знак интеграла:
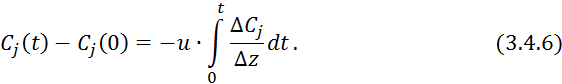
Продифференцируем по времени левую и правую часть:

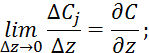

Ввиду поршневого течения вещества данное уравнение справедливо для всего потока:

Так как это уравнение является уравнением в частных производных, то МИВ является моделью с распределенными параметрами.

3.4.10 преобразуем по Лапласу по времени, получим:
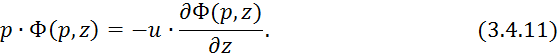
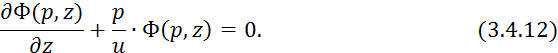
Уравнение 3.4.12 имеет решение:
![]()
полагаем z=0: ![]() .
.
Таким образом, 3.4.13 примет вид:
![]()
полагаем ![]() :
:
![]()
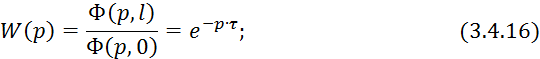
![]()
Построим ![]() и
и ![]() кривые:
кривые:
![]()
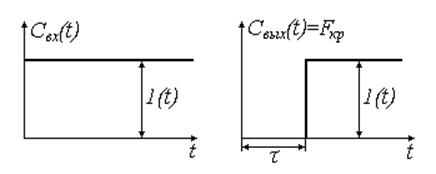
Рис. 22
![]()
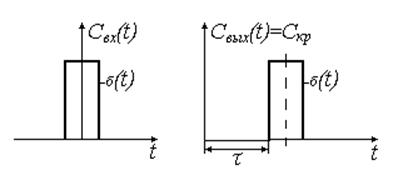
Рис. 23
Модели
идеального вытеснения наиболее соответствуют трубчатые вещества при
турбулентном течении вещества и ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.