Методы моделирования объектов и систем управления. Математическое описание тепловых процессов. Методы и алгоритмы идентификации динамических систем. Оптимизация химико-технологических с использованием математических моделей, страница 30

2)  Определяется приращение  , .

3)  На каждом шаге вычисления сравнивается , если условие выполняется, то делается следующий шаг, если нет, то считается, что величина  и .

Достоинство: простота реализации.

Недостаток: при большой точности необходимо делать большое количество шагов, то есть точность заливист от .

Б)  Метод поразрядного приближения.

Данный метод является разновидностью метода равномерного поиска и реализуется по следующему алгоритму:

1)  Создается начальное приближение  и здесь же задается величина шага .

2)  Добавляем  и вычисляем значение .

3)  На каждом шаге производим сравнение . Если данное условие выполняется, то переходим к п.2, если нет, то переходим к п.4.

4)  ; , где  — заданная погрешность вычисляется.

Если данное условие выполняется, то переходим к п.2, если нет, то считается, что найден экстремум функции в точке , .

В)   Метод квадратичной интерполяции.

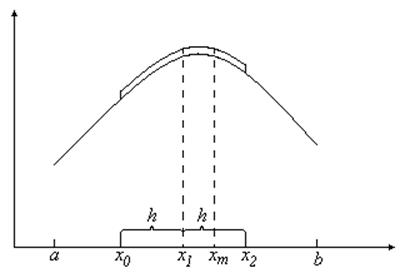
Рис. 51

Сущность.

Задается значение  внутри интервала

Алгоритм реализации следующий:

1)  Задается значение  на интервале поиска, задается  и вычисляется , ;

2)  Вычисляется , , .

3)  Вычисляются коэффициенты параболы

 

по следующим формулам:

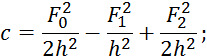
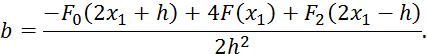
и далее определяем величину экстремума:

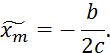
4)  Составляется неравенство:

Если неравенство выполняется, то принимается  и вычисляется , если не выполняется, то переходим к п.1 приняв .

Г)   Метод дихотомии.

Метод заключается в делении отрезка  пополам и реализуется следующий алгоритм:

1)  Проверяется условие , где  — погрешность. Если условие выполняется, то переходим к п.6, если нет, то к п.2.

2)  .

3)  Вычисляем  и .

4)  Сравниваем . Если условие выполняется, то полагаем, что  и переходим к п.1, если не выполняется, то переходим к п.5.

5)   и переходим к п.1.

6)  Вычисляем  и .

Сравнение методов показывает, что для простоты целевых функций  может быть использован метод поразрядного приближении; для более сложных — метод квадратичной интерполяции.    

Д)   Метод многомерной оптимизации.

Необходимо найти , которые обеспечивают максимум целевой функции.

Метод покоординатного спуска (при поиски минимума).

Метод покоординатного схождения (при поиске максимума).

Для поиска минимума по каждой координате применяются перечисленные выше методы. По всем координатам поиск осуществляется одинаковым шагом.

9.5.  Реализация методов оптимизации в пакете MatLab (toolbox)

9.5.1  Оптимизация (минимизация) функции

Задания:

1)  Поиск минимума функции одной переменной для фиксированного интервала.

2)  Поиск минимума функции нескольких переменных без ограничений:

— симплекс-метод;

—  метод градиентного поиска.

3)  Поиск минимума функции нескольких переменных с ограничениями.

4)  Решение задач линейного программирования.

5)  Решение задач квадратичного программирования.

Решение:

1)  Поиск минимума функции  одной переменной для фиксированного интервала.

Найти минимум функции:

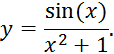
Для нахождения минимум функции используем команду fminbnd.

Создаем встроенную функцию:

f unction y=kate (x)

y=sin(x)/x^{^}2+1 %значение функции

В новом окне находим минимум функции с помощью команды fminbnd:

clc,clear% очистка окна х0=[-10;10)% интервал, в пределах которого ищем минимум функции

[x,f]=fminbnd ('kate',x0)

где:

х — значение переменной в точке минимума;

f — значение функции в точке минимума.

2)  Поиск минимума функции  нескольких переменных без ограничений.

Найти минимум функции:

1)  Симплекс-метод:

Создаем встроенную функцию:

function y=kate(x)

у-ехр(х(1))*(4*(х(1))^{^}2+2*(х(2))^{^}2+4*х(1)*х(2)+2*х(2)+1) % значение функции

В новом окне при помощи команды fminsearch находим минимум функции: clc,clear% очистка окна х0=[-1;1] % %вектор начальных значений

[x,f,h]=fminsearch(' kate',xO) где:

х — значение переменной в точке минимума;

f — значение функции в точке минимума;