Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата

Дискретная математика состоит из набора различных математических наук.

Это математическая логика, теория алгоритмов, теория графов и т.д. Некоторые разделы дискретной математики Вы будете изучать в этом (четвертом) семестре, а некоторые (например, комбинаторика и вероятность, математическая логика и теория алгоритмов, теория кодов) – в 5, 6 и 9 семестрах  в курсах

«Теория вероятностей и математическая статистика», «Математическая логика и теория алгоритмов», «Кодирование и передача информации».

ТЕОРИЯ МНОЖЕСТВ

Одним из основных понятий математики является понятие множества.  Под  множеством понимается вполне определенная совокупность объектов или элементов, которые рассматриваются как единое целое. Определить множество – это значит указать, какие элементы некоторого универсального класса объектов входят в него, а какие не входят. 

Множества обычно обозначают  большими буквами, а элементы, принадлежащие множеству, записывают между двумя фигурными скобками.

Если порядок расположения элементов несущественен, то множество называется неупорядоченным. В неупорядоченном множестве не может быть одинаковых элементов.

Замечание:  Языки программирования требуют, чтобы каждая переменная  была отнесена к одному  из типов данных. Тип данных – это множество объектов со списком операций над ними. Объявление типа переменной равносильно указанию множества, из которого переменной присваиваются значения.

Способы задания множеств:

- перечислением элементов, например,  . Очевидно, что метод удобен при малом числе элементов;

- указанием характеристического свойства , Эта запись означает, что множество  состоит из элементов , которые обладают указанным свойством;

Примеры:

, ,

- с помощью порождающей процедуры, которая указывает способ получения элементов множества из уже полученных элементов множества или из других объектов. Пример:  Множество С  задается порождающей процедурой со следующими правилами: 

-цифра 1, 

-если , то .

Легко увидеть, что это множество  всех целых чисел, являющихся степенью числа два:     

Принадлежность элемента   к множеству  записывается как . Если  не является элементом множества , то пишут .

Существуют конечные и бесконечные множества. Особое множество – это пустое множество. Оно не содержит ни одного элемента, например  . Обозначается пустое множество символом Æ. Обратите внимание, что это не ноль, а также что  Æ.

Множества и подмножества

Множество  является подмножеством множества ,  (Обозначается ), если каждый элемент  является элементом множества , т.е. если , то . При этом говорят, что  содержит .  Пример:

Символ  называется символом включения.

Множества равны, если содержат одни и те же элементы. Пример:

, . Ясно, что .

Для равных множеств выполняется  и  (такое определение равенства множеств обычно используют для доказательства равенства множеств).

Если  и то  иногда называют собственным, строгим или истинным подмножеством  (Обозначается ). Символ называется символом строгого включения. Пример: ,   . Ясно, что .

Универсальное множество  это множество, обладающее таким свойством, что все рассматриваемые множества являются его подмножествами.

Удобным способом изображения множеств являются диаграммы Эйлера-Венна. Прямоугольником изображается универсальное множество, а остальные множества – окружностями и фигурами, полученными от пересечения, объединения и т.д этих окружностей.

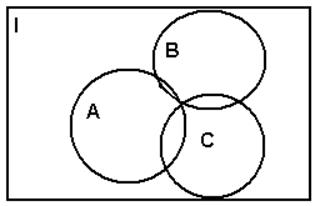
Операции над множествами

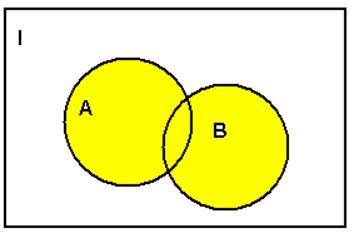
Операция объединения. Объединением множеств  и  называется множество, которое включает в себя все элементы множества  и все элементы множества  (Обозначается ).

 или

Пример: ,  , тогда

Если система множеств состоит  из нескольких множеств , то можно записать  .

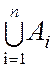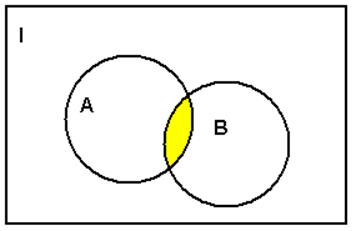
Пересечением множеств  и  называется множество, состоящее из элементов принадлежащих и множеству  и множеству .

 и . Множество, являющееся пересечением нескольких множеств удобно записывать выражением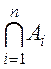  

Пример: ,  , тогда .

Могут существовать и непересекающиеся множества, когда Æ.

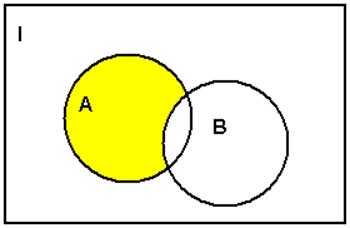
Разность множеств.  Разностью множеств  и  называется множество, которое состоит из тех элементов множества , которые не содержаться в множестве .   и .

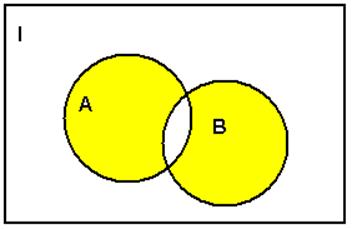
Симметрическая разность множеств определяется выражением , т.е. элементы этого множества принадлежат либо множеству , либо множеству , но не обоим множествам вместе.

Дополнением множества   называется множество элементов универсального множества не принадлежащих множеству :   

Тождества алгебры множеств

Используя операции над множествами можно получать выражения, определяющие другие множества. Два выражения можно назвать тождественными, если они определяют одно и то же множество.

Для доказательства можно взять произвольный элемент одного множества и показать, что он принадлежит и другому множеству.

Пример: Докажем справедливость равенства

Шаг 1: Возьмем элемент , из определения разности множеств следует, что  и ;

Шаг 2: поскольку , то , т.е.  и

Шаг 3: воспользовавшись определением пересечения множеств,  окончательно запишем .