Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 11

Если  еще существует путь из  истока  к стоку  содержащий только ненасыщенные дуги, то процесс повторяем, если таких путей нет, то суммируя потоки в  найденных путях получаем величину полного потока.

Этап 2. Нахождение наибольшего потока.

Системы исчисления.

Системой исчисления называется способ изображения любых чисел с помощью ограниченного количества символов. Число этих символов определяет основание системы счисления.

Примеры:

В двоичной системе счисления используются два символа: 0, 1;

в десятичной системе счисления - десять символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; в шестнадцатеричной системе счисления – 16 символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

В любой позиционной системе счисления с основанием  число  равно:

 

целая часть числа                                 дробная часть числа

Рассмотрим вначале целые числа. Количество символов, использованное для изображения конкретного числа, определяет разрядность числа. Младший (нулевой) разряд пишется справа.

В позиционных системах счисления вклад символа в изображаемое число зависит не только от самого символа, но и от положения этого символа в числе. Этот вклад равен , где  - символ в  разряде числа,  - основание системы счисления. Например:

, т.е. младший разряд определяет число единиц, а последующие – число десятков, сотен, тысяч.

Если ведется работа с числами, изображаемыми в различных системах счисления, то следует указывать основание системы счисления. Обычно это делают, записывая после числа основание системы счисления: (B) – двоичная,

(О) – восьмеричная, (D) –десятичная, (H) – шестнадцатеричная. Иногда основание системы счисления приписывают к изображаемому числу в виде нижнего индекса: , , . 

Пример: запишем число 1000. В зависимости от основания системы счисления  это число будет соответствовать различным десятичным эквивалентам:

1011(В) соответствует десятичному числу 11, т.к. ;

1011(О) соответствует десятичному числу  521: ;

1011(D) – это число 1011: ;

1011(H) – соответствует десятичному числу 4113:                  .

Перевод целого числа из десятичной системы счисления в систему с другим основанием проводят последовательно деля число на основание требуемой системы счисления. Деление продолжается до тех пор, пока остаток не станет меньше основания новой системы счисления. Число в новой системе записывается в виде остатков от деления, начиная от последнего остатка, снизу вверх.

Пример: пусть имеется целое десятичное , которое нужно перевести в двоичную систему счисления. Поскольку  и , после деления  на основание системы счисления 2 мы получим новое число 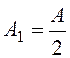 и остаток от деления :

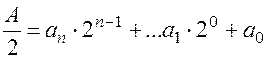, где  - младший разряд двоичного числа.

 

Теперь делим на 2 число  и находим значение следующего разряда двоичного числа :

.

 

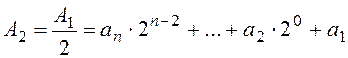Деление продолжается до тех пор, пока не получим в остатке 1, являющуюся старшим разрядом двоичного числа.

Пример: 49:2=24 + остаток 1 (это разряд  искомого двоичного числа),

24:2=12 + остаток 0 (разряд ),

12:2=6 + остаток 0 (разряд ),

6:2=3 + остаток 0 (разряд ),

3:2=1 + остаток 1 (разряд ), т.к. 1 на 2 не делится, то это разряд  двоичного числа. Окончательно 49(D)=110001(B).

Пример: Перевести десятичное число 110 в шестнадцатеричную систему счисления. 110:16=6 + остаток 14. В шестнадцатеричной системе счисления 14 изображается символом E. Итак, 110(D)=E6(H).

Рассмотрим теперь задачу перевода десятичного числа  в другую систему счисления . Эта задача сводится к определению неизвестных коэффициентов . Для их нахождения будем умножать  на основание системы счисления :

. В результате мы получаем  первый                     разряд после запятой искомого числа и остаток , который является дробным числом. Умножая полученный остаток на  

определяем   второй разряд после запятой и новый остаток . Умножение осуществляется до тех пор, пока дробная часть не станет равной нулю (точное преобразование), либо пока не получится достаточное количество разрядов искомого числа с точки зрения точности преобразования.