Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 31

Д - триггер.

1, 2  - сигналы на выходе Q верхнего и нижнего триггера соответственно.

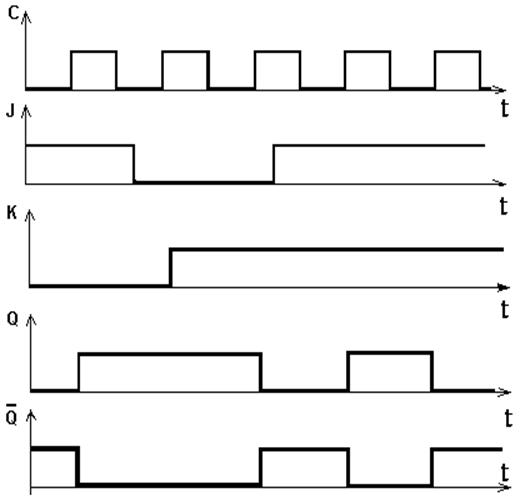
J - K триггер.

J – управляющий вход устанавливающий триггер в единицу;

K – управляющий вход устанавливающий  триггер в ноль;

С – синхровход.

Cинтез функциональной схемы конечного автомата     

Задачу синтеза конечного автомата к задаче синтеза комбинационных схем. Вы уже знаете, что структура конечного  С-автомата имеет вид:

Если  синтезировать комбинационные схемы  входящие в эту структуру, то можно начертить функциональную схему конечного автомата. Для этого следует определить, сколько входных и выходных проводников в каждой из комбинационных схем. Каждому входному проводнику  соответствует аргумент булевой функции, а на каждом выходном проводнике формируется значение булевой функции. Таким образом, число выходных проводников определяет число функций, которое реализует комбинационная схема, а число входных проводников определяет число аргументов, от которых зависят эти функции.

Для определения числа входных шин конечного автомата (они являются частью входов первой и второй комбинационных схем), выходных шин 1-го рода, 2-го рода, числа элементов памяти используют формулу , где ]  [ -означает  округление к большему целому.

1) количество входных проводников конечного автомата:

 - число входных шин,

-число входных сигналов конечного автомата (число элементов в множестве , т.е. мощность множества ).

2) число выходных шин 1-го рода (число выходных проводников комбинационной схемы 2):

 - число выходных шин 1-го рода,

 - мощность множества .

3) число  выходных шин 2-го  рода (число выходов комбинационной схемы 3):

 - число выходных шин 2-го рода,

 - число выходных сигналов 2-го рода абстрактного автомата (мощность множества ).

4) число элементов памяти:

 - число элементов памяти,

 - число состояний автомата (мощность множества ).

После этих вычислений производится кодирование входных, выходных сигналов и состояний автомата. При этом каждому символу входящему в множества  ставится в соответствие кодовая комбинация на соответствующих входных, выходных шинах  а также на элементах памяти.

Замечание. На практике в ряде случаев коды входных и выходных сигналов задаются заказчиком.

Пример. Синтезируем С – автомат, заданный таблицей переходов и таблицей выходов. Будем использовать логические элементы булевого базиса, уравнения представлять в дизъюнктивных формах, а в качестве элементов памяти  используем Т – триггеры.

Таблица переходов – выходов автомата:

Множество  содержит два элемента, поэтому комбинационная схема 1 автомата имеет один входной проводник. Пусть 0 на этом проводнике соответствует , а единица - .

Автомат имеет 3 состояния, следовательно,  нужны 2 триггера (). Состояние конечного автомата определяет состояние этих триггеров. Примем, что если первый триггер находится в нуле, а второй триггер в единице, то это будет состояние  (Говорят, что состоянию  приписан код 01). Продолжаем кодирование состояний. Припишем состоянию  код 10, а состоянию  код 00.

Замечание 1. Естественно, что проектировщик может выбрать  для кодирования состояний и другие коды.

Замечание 2. От выбранных кодов зависит сложность комбинационной схемы 1.

У автомата 3 типа выходных сигналов 1-го рода, следовательно, он имеет 2 выходных проводника 1-го рода. Пусть сигналы 00 на этих проводниках соответствуют ; 01 –соответствуют ; 10 – .

Комбинационная схема 3 имеет один выходной проводник. Пусть 0 на этом проводнике соответствует сигналу , а 1 – сигналу .  

Теперь нужно заменить символы  в абстрактной таблице переходов–выходов на соответствующие коды  и получить кодированную таблицу переходов-выходов: