Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 16

0	0	0	1	1	1	0	0	0	0
0	0	1	1	0	1	0	1	0	*
0	1	0	*	0	1	1	0	1	*
0	1	1	*	0	1	1	1	0	0

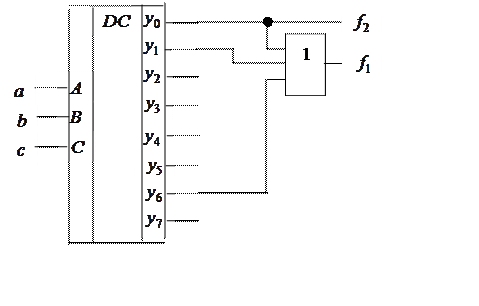
Функции  и  зависят от трех аргументов, следовательно, необходим дешифратор  с тремя входами. Особенностью этих функций является то, что они заданы не на всех наборах. Такие функции называют не полностью  определенными булевыми функциями. Наборы,  на которых функция не определена, помечены символом *. Эти функции необходимо доопределить, т. е. приписать функциям нам этих наборах значения 0 или 1.

Доопределение проводят таким  образом, чтобы получить наиболее простую схему. Для данного примера выгодно доопределить эти наборы нулями.

 

Существуют дешифраторы с инверсными выходами. Схема такого дешифратора имеет вид:

 

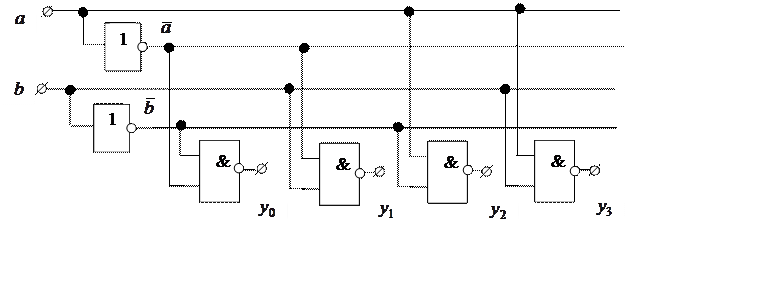Запишем уравнения для этого дешифратора:

,  , ,  . Построим таблицы истинности для этих уравнений:

					Видно, что такой дешифратор формирует на своих выходах все конституенты нуля булевых функций двух аргументов: , , , , ,.
0	0	0	1	1	1
0	1	1	0	1	1
1	0	1	1	0	1
1	1	1	1	1	0

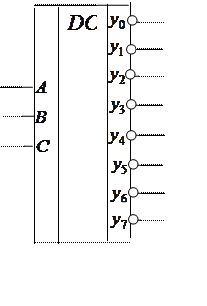          Условные графические обозначения дешифраторов с инверсными выходами отличаются от дешифраторов с прямыми выходами наличием значков инверсии на выходах:

входами:

 

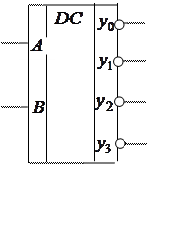Такие дешифраторы являются генераторами конституент нуля и позволяют реализовывать булевы функции путем перемножения конституент нуля. Если реализовать функции из предыдущего примера на таких дешифраторах, то получим схему:

                                                 

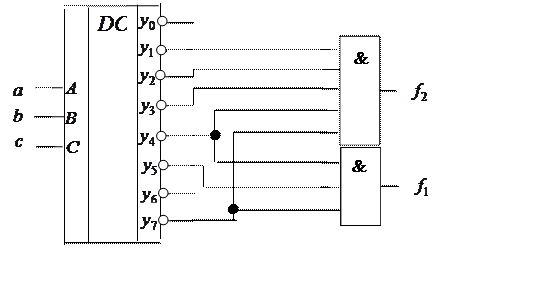
Мультиплексоры.

Проведем анализ еще одной простейшей схемы, которую называют

мультиплексором:

 

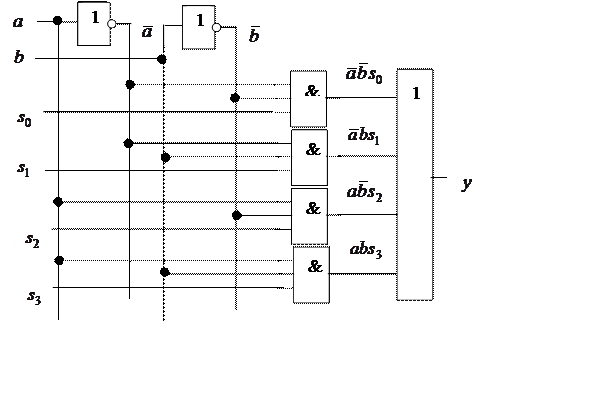Запишем уравнение для выходного сигнала мультиплексора:

. Функция зависит от шести аргументов, поэтому таблица истинности будет слишком громоздкой. Вычислим значения функции, задавая только значения  и :

		Входы   и  мультиплексора называют адресными, а входы , , ,  -селектируемыми. Из таблицы видно, что мультиплексор подключает к своему выходу один из селектируемых входов, номер которого определяется кодом на адресных шинах.
0	0
0	1
1	0
1	1

Число селектируемых входов равно , где  - число адресных входов.

В литературе тип мультиплексора часто задают обозначением , здесь  - число селектируемых входов мультиплексора, которые коммутируются на 1 выход. Существуют мультиплексоры 2x1, 4x1, 8x1, 16x1, 32x1 и т.д. Мы рассмотрели мультиплексор 4x1. Принцип работы других мультиплексоров подобен работе мультиплексора 4x1. Например функционирование мультиплексора 8x1 можно пояснить аналогичной таблицей:

	0	0	0	0	1	1	1	1
	0	0	1	1	0	0	1	1
	0	1	0	1	0	1	0	1

Постройте самостоятельно подобные таблицы для мультиплексоров 2x1 и 16x1.