Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 15

Алгоритм перехода к ДСНФ:

- Выбрать в таблице истинности все наборы на которых функция равна единице.

- Записать конституенты 1 равные единице на этих наборах. При этом, если аргумент в наборе равен 1, то в конституенту единицы этого набора он записывается без отрицания. Если же аргумент в наборе равен нулю, то он записывается с отрицанием.

- Полученные конституенты соединить операцией дизъюнкции.

Определение: конституентой нуля называют дизъюнкцию всех переменных, записанных с отрицанием или без него.

Любая конституента нуля равна нулю только на одном наборе, на остальных наборах она равна 1.

Теорема. Любая булева функция может быть записана как конъюнкция конституент нуля, записанных для наборов,  где функция равна нулю.

Доказательство. Выбираем в таблице истинности произвольный набор. Если на этом наборе функция равна нулю, то записываем конституенту нуля равную нулю на этом наборе. Поскольку  свойство конъюнкции , то на данном наборе функция будет равна нулю. Если же функция равна на наборе 1, то конституенту нуля равную нулю на этом наборе не выписываем, а т.к. остальные конституенты на этом наборе равны 1, то и их произведение будет равно 1. Такая запись булевой функции называется конъюнктивной совершенной нормальной формой (КСНФ).

Алгоритм перехода к КСНФ:

-Выбрать в таблице истинности наборы на которых функция равна нулю.

-Записать конституенты нуля равные нулю на этих наборах. Для этого, если аргумент набора равен нулю, то он входит в конституенту без отрицания, если же аргумент входит в набор как 1, то в соответствующую конституенту нуля вписывается его отрицание.

-Все записанные конституенты нуля соединяем знаком конъюнкции.

Запишем КСНФ для функции из предыдущего примера:

.

Дешифраторы.

При работе с дискретными устройствами приходится решать задачи анализа схем и задачи синтеза схем. При решении задачи синтеза после получения технического задания на проектирование устройства составляется математическая модель устройства, а затем разрабатывается схема устройства. Задача анализа обратная задаче синтеза. Решим задачу анализа, рассматривая схему простейшего дешифратора с прямыми выходами. 

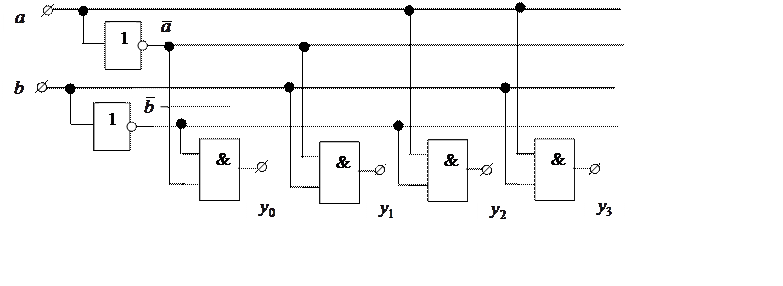
В схеме два входа ,   и четыре выхода, которые описываются булевыми уравнениями: ,  ,  ,  . Построим таблицы истинности для этих уравнений:

					Видно, что такой дешифратор формирует на своих выходах все конституенты единицы булевых функций двух аргументов: , , , .
0	0	1	0	0	0
0	1	0	1	0	0
1	0	0	0	1	0
1	1	0	0	0	1

Итак, если на вход дешифратора подать аргументы булевой функции, то на выходах дешифратора можно получить все конституенты 1. Число входов дешифратора  связано с числом выходов  соотношением .  Дешифраторы  с двумя, тремя, четырьмя и т.д. входами можно рассматривать как генераторы конституент единицы для функций 2, 3, 4, и т.д. аргументов. Суммируя конституенты 1 для наборов, где функция равна 1, мы получаем реализацию этой функции.

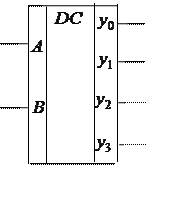
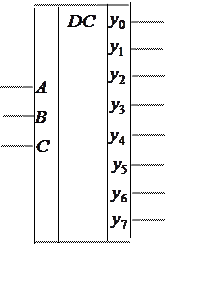          Приведем условные графические обозначения ( УГО) дешифраторов с 2 и 3 входами:

Пример: реализовать систему булевых функций на дешифраторе с прямыми выходами.