Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 2

Другим способом проверки тождественности, является использование диаграмм Эйлера-Венна. Если построить диаграмму для множества, описываемого левой частью, а затем – диаграмму для множества, определяемого правой частью, то совпадение диаграмм свидетельствует о том, что мы имеем дело с одним и тем же множеством. Так, например,  для предыдущего равенства диаграммы для левой и правой частей одинаковы и имеют вид

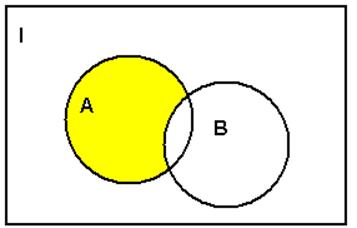
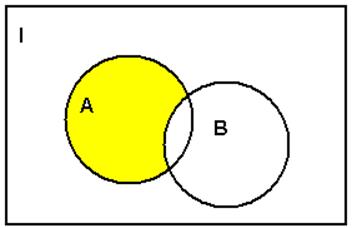
Ниже приведены некоторые тождества теории множеств, которые могут быть выведены путем формальных доказательств, либо проверены с помощью диаграмм Эйлера-Венна:

;      -законы идемпотентности.

 -правило двойного дополнения.

;   - правила де Моргана.

;   - свойства коммутативности.

  - свойства ассоциативности.

.

 - свойства дистрибутивности

.

Æ; Æ=Æ; ;  - свойства тождества.

; Æ - свойства дополнения.

Формула включений и исключений

Множества различаются по количеству входящих в них элементов. Число элементов в конечном множестве   называют мощностью множества  и обозначают ç ç.

Подсчитать число элементов во множестве можно с помощью методов комбинаторики, которая будет изучаться в следующем семестре.

Теорема включений  и исключений позволяет вычислить мощность объединения множеств:

.

Докажите эту теорему самостоятельно.

Упорядоченные множества

В предыдущих примерах рассматривались множества, в которых порядок расположения элементов не существенен, поэтому множества  и  считались равными. В упорядоченных множествах это не так.

Упорядоченным множеством или кортежом называется совокупность элементов, в которой каждый элемент занимает определенное место. Примерами кортежей являются последовательность букв в слове, координаты точки пространства, очередь. В этих множествах место каждого элемента не может быть изменено. Число элементов кортежа называется его длиной.  Для того чтобы отличать упорядоченные множества от неупорядоченных,  применяют круглые скобки

Обратите внимание, что в отличие от неупорядоченного множества в кортеже могут быть одинаковые элементы  (например, точка пространства с одинаковыми координатами по различным осям).

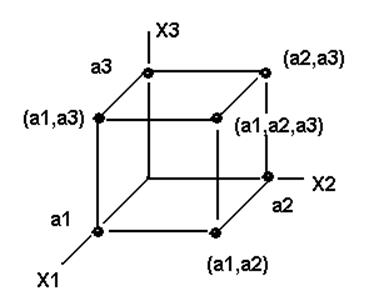
Если рассматривать точку трехмерного пространства , то компоненты   будут проекциями точки на оси X1,X2,X3 соответственно ,   , .

Можно рассматривать проекции этого кортежа сразу на две оси, т.е. на координатную плоскость, естественно, что она будет представляться уже упорядоченным множеством - двухэлементным кортежом:    , .

Еще одним примером упорядоченного множества служит декартово произведение множеств  и . Декартовым произведением  является множество, состоящее из упорядоченных пар , таких, что первый компонент пары принадлежит множеству , а второй – множеству :

 и .  Порядок следования компонент в паре существенен. Естественно, что если  и , то .

Пример прямого произведения множеств: -множество водителей, - множество автомашин, тогда

- состоит из всевозможных пар (водитель, автомобиль):

.

Если  содержит  элементов, а  -  элементов, то    содержит  элементов. Если  пусто, или  пусто, то  также пусто.

Прямое произведение множеств может состоять из любого числа множеств.

Теорема: Если - конечные множества с мощностями , то мощность множества  равна произведению мощностей

:     ç ç.

Частным случаем прямого произведения множеств является степень множества .  Считают, что , Æ.

Примеры:

Если , то .

Если же  - множество вещественных чисел, то  трехмерное вещественное пространство.

Проекция множества.

Данное понятие применяется только для множеств, состоящих из кортежей одинаковой длины. Проекцией множества на ю ось называют множество, состоящее из х элементов всех кортежей, входящих в множество .

Пример: , тогда ,

,

Рассмотрим еще один пример:

Пусть  ,  ,

Отношения

Абстрагирование от всех свойств реальных объектов, кроме одного свойства, объединяющего их в целое, приводит к понятию множества. Однако помимо самих объектов имеются и связи между объектами. В теории множеств эти связи могут быть представлены в виде отношений между отдельными элементами множеств.