Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 29

В общем случае абстрактный автомат имеет 1 входной и 2 выходных канала. Такой автомат называют С-автоматом.

         

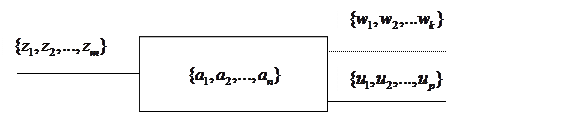
В каждый момент времени  автомат находится в определенном состоянии . При  - в начальном состоянии .

Автомат, находящийся в состоянии   воспринимает входной сигнал , выдает на выход 1-го рода сигнал , выдает на выход 2-го рода сигнал  и переходит в следующий момент времени в состояние .

.

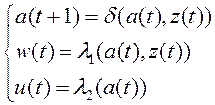         Типы конечных автоматов.

Кроме рассмотренного выше С-автомата на практике получили распространение автоматы Мили и автоматы Мура.

Автомат Мили

Выходные сигналы автомата Мили - сигналы первого рода. Память автомата характеризуется множеством внутренних состояний автомата. Указывается (обязательно) состояние с которого автомат начинает работу  - начальное состояние.

Алгоритм работы задается функцией переходов и функцией выходов первого рода:

.

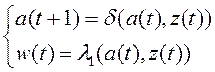Автомат Мура

 

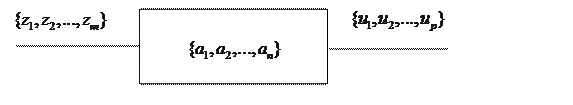
Выходные сигналы автомата Мура - сигналы второго рода. Алгоритм работы задается функцией переходов и функцией выходов второго рода:

                              Методы задания конечных автоматов

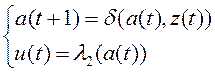
Наиболее распространены табличный способ задания конечного автомата и представление автомата с помощью ориентированного связанного графа.

Табличное задание автомата Мили

При табличном способе задания в верхней строке перечисляются все состояния конечного автомата, а в левом столбце – все входные сигналы. В верхних треугольниках пишут состояние в которое должен переключиться автомат в соответствии  с заданным алгоритмом функционирования, в нижних треугольниках записывают значения выходных сигналов 1 рода.

Пример:

При построении граф-схемы вершины графа соответствуют состояниям автомата переключение показывается направленными дугами в начале ставится входной сигнал вызывающий переключение, в конце дуги формирующийся выходной сигнал.

Иногда таблицы функционирования автомата представляются в другом виде:

Табличное задание автомата Мура

Две верхние  строки задают функцию выходов 2-го рода, а вторая строка и оставшаяся часть таблицы – функцию переходов.

Пример:

 

Табличное задание С - автомата

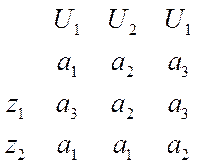
В задании на контрольную работу автомат задан двумя таблицами: таблицей переходов и таблицей выходов.

При синтезе конечных автоматов решается задача абстрактного синтеза конечного автомата, а затем задача структурного синтеза автомата. Целью абстрактного синтеза является получение математической модели автомата по техническому заданию и упрощение этой модели. Математическая модель может быть представлена графом автомата, либо таблицей переходов – выходов.

Пример. Синтезировать управляемый генератор периодической последовательности прямоугольных импульсов. Если управляющее входное напряжение равно нулю, то на выходе генератора – ноль. Если управляющее входное напряжение равно единице, то на выходе генератора формируется периодическая последовательность прямоугольных импульсов. Период имеет вид 11010.

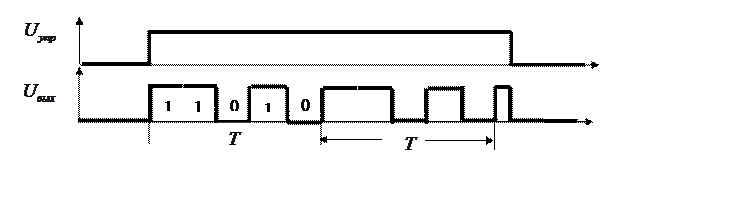
Проведем абстрактный синтез этого автомата. Возьмем модель Мили. Для задания конечного автомата нам необходимо  определить множества входных сигналов, выходных сигналов, множество состояний, в котором необходимо указать начальное состояние, а также определить функцию переходов и функцию выходов первого рода. Множество входных сигналов состоит из двух элементов,  и . Множество выходных сигналов также состоит из двух элементов  и. Из этих сигналов  можно скомпоновать любую последовательность прямоугольных импульсов. Комбинация выходных сигналов  образует необходимый нам период 11010.