Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 5

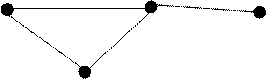
                     a              5         b          9        c

14              10

d

Бинарные операции на графах

Пусть даны два графа  и .

Операцией объединения  и  называют граф  такой, что

 и .

Операцией пересечения  и  называют граф  такой, что

 и .

Пример:              

                                         

a       b           c                     b         a        d 

                                         

, ;     ,

После выполнения операций объединения и пересечения получим: 

a        b      c        d                    a          b

 

Соединения графов состоит из  и всех ребер, соединяющих

 и . Если выполнить операцию соединения для графов  и , то получим  :

                                                       d

a              b                  c

Композиция графов. . Операцию композиции можно выполнять в случаях, когда графы имеют общие вершины.

Пример:

                                    a                                a

c             b                 c                     b

                             

, ;    ,

                       a

c               b

Композицию двух графов можно найти перемножая матрицы смежности графов:

   0 1 1               0 0 0                1 1 1

0 0 0       Ä     1 0 1     =       0 0 0                           

1 0 0               0 1 0                0 0 0

Поясним  способ перемножения. Пусть  - элементы перемножаемых матриц,   - элемент результирующей матрицы, где  - номер строки,  - номер столбца. Вычислим, например, элемент  :

           При вычислениях используют операции булевой арифметики, которая  использует операции сложения и умножения определенные следующим образом: , , , , .

Использование булевой арифметики позволяет не выходить за пределы множества чисел .

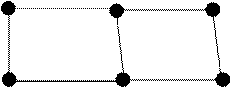
Граф  называется подграфом графа , если он построен на подмножестве вершин исходного графа  и содержит только те ребра, которые начинаются и заканчиваются в данном подмножестве.

                                                                             a                  b              c

Для графа, показанного на рисунке справа построим несколько подграфов:                

d                   e               f

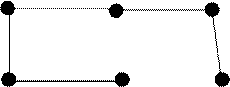a                   b               c                              a                  b              c                              

 

                                                       

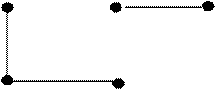d                   e              f                                d               e

В ориентированном графе путем называется такая последовательность дуг, в которой которой конец предидущей дуги совпадает с началом последующей дуги.

Путь называется простым путем, если в его изображении ни одна вершина не встречается более одного раза.

Путь в котором начальная и конечная вершина совпадают, называется контуром.

Для неориентированного графа вводят понятия цепи и цикла. Под цепью понимают последовательность ребер. Вершины цепи, степень которых равна единице, называют концевыми вершинами.

Цепь, концевые вершины которой совпадают, называется циклом.

v1                           v2                                                 x1                        x2

 

v4                                           x3                             x4

v3

 - путь длины 4;  простой путь длины 3;  - цепь длины 5, - простая цепь; - простой цикл.

Вершина  называется достижимой из вершины , если существует направленный путь из вершины  в .

Вершина  называется контрадостижимой из вершины , если существует направленный путь из вершины   в  .

На практике часто возникает задача определения множества всех вершин графа, достижимых из заданной вершины . Обозначим  -множество всех вершин достижимых из  с использованием путей длины 1;  - множество вершин достижимых из  с использованием путей длины 2 и т.д. Тогда для решения задачи достаточно найти объединение множеств . Это объединение называется транзитивным замыканием вершины  и обозначается . Для конечных графов число членов объединения конечно. Степень   не превышает длины самого большого простого направленного пути в графе с началом в вершине .